机器学习：贝叶斯分类算法

发表于 2021-12-24 分类于机器学习本文字数： 898

贝叶斯定理

$P (X | C_{i})$ 表示 X 在类别 i 下的条件概率

P (C_{i} | X) = \frac{P (X | C_{i})}{P (X)} P (C_{i})

$P (X | C_{i})$ ：

此处的 X 是一个属性的取值。

贝叶斯决策的准则为：

若对任意的 j 和特定的 i

P (C_{i} | X) > P (C_{j} | X)

则 X 属于类别 i

假设 X 属于类别 c , $P (c)$ 代表类别 c 的概率， $P (X)$ 表示的是样本 X 的概率， $P (X | c)$ 表示一个物品是 c 类别的情况下它是 $X$ 的概率，则可以求出这个物品是 X 的情况下他是 c 类别的概率

P (c | X) = \frac{P (X | c)}{P (X)} P (c)

但是类别不至有一个，找到物品确定是 X 的情况下，最有可能属于的类别需要这样子计算：

m a x (P (c_{i} | X)) = m a x \frac{P (X | c_{i}) P (c)}{P (X)}

也就是遍历所有类别，一个一个算，求出里面最大概率的情况下的 $c_{i}$ 就被称为 极大后验假设，记作 $c_{m a x}$ 也就是

c_{m a x} = a r g m a x_{c \in C} \frac{P (X | c_{i}) P (c)}{P (X)}

由于是求最大，不是求具体的数值，所以可以忽略共同因子 $P (X)$

在没有类别概率 $P (c)$ 的情况下，可以假设每个类别的概率相等，所以再忽略 P©

c_{m l} = a r g m a x_{c \in C} P (X | c)

这就是极大似然概率

朴素的假设：属性的类条件独立性。就是在指定类别的时候，属性之间是相互独立的。

X 由属性 ${x_{1}, x_{2}, . . ., x_{n}}$ 组成

想根据贝叶斯公式求解最大后验假设，我们需要先有 $P (X | C_{i})$ 和 $P (C_{i})$

由于朴素假设，所以可以直接计算（所有属性的条件概率累乘）

P (X | C_{i}) = \prod_{j = 1}^{n} P (x_{j} | C_{i})

最大后验假设：

i_{m a x} = a r g m a x_{i \leq m} P (C_{i}) \prod_{j = 1}^{n} P (x_{j} | C_{i})

这就是朴素贝叶斯分类器进行分类的依据，类别 $i_{m a x}$ 就是样本 X 所属的类别。

工作过程：

遍历所有样本 X ，根据朴素假设下的贝叶斯定理，将 X 判断为最大后验假设的那个类别。

如果 $P (C_{i})$ 未可知，则假设他们相等（在计算中可以直接忽略），也可以用样本中 $C_{i}$ 所占的比例对 $P (C_{i})$ 进行估算。
如果属性 $A_{k}$ 是连续值，则假设它服从正态分布；如果是离散的，则按照样本中，指定类别下该属性为指定值的比例来计算 $P (x_{j} | C_{i})$

算法描述：

朴素假设太严格

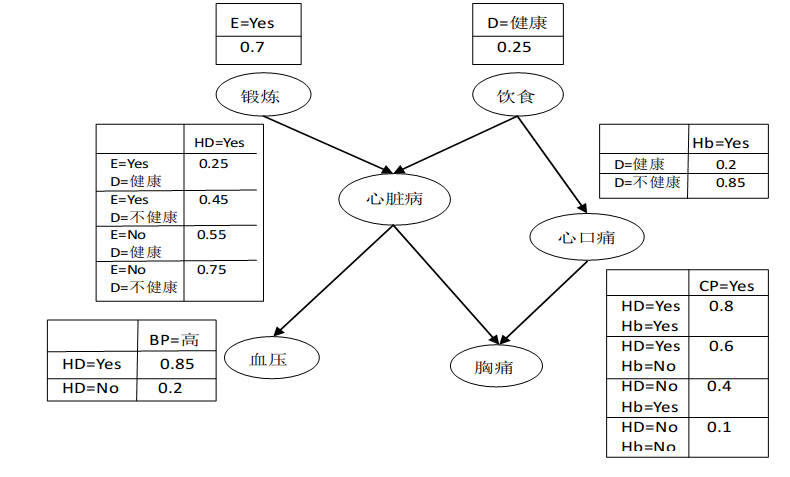
用图形表示一组随变量之间的概率关系: