编译原理:词法分析
参考:中国大学 MOOC 国防科技大学 编译原理
功能
输入源程序、输出单词符号
单词的种类
-
基本字(关键字)
-
标识符
-
常数
-
运算符
-
界符
单词表示形式
< 种别, 单词自身的词 >
-
种别通常用整数编码表示
- 基本字、运算符、界符一符一种
- 标识符单列一种
- 常数按类型分种
正规集与正规式
-
和 都是 上的正规式,他们所表示的正规集为 和 -
对任意的
, 为其上的正规式,表示的正规集为 -
设
和 为 上的正规式,表示的正规集分别为 和 为正规式,表示的正规集为 为正规式,表示的正规集为 (集合的连接) 为正规式,表示的正规集为 - 由有限次使用上述 3 步骤定义的表达式才是正规式,这些正规式表示的字集才是正规集
等价
两个正规式的正规集相同
如:
FA 有限自动机
DFA 确定有限自动机
S 为有穷状态集,
状态转换函数:
s 状态下接收 a 转化为 s’
NFA 非确定有限自动机
S 为有穷状态集,
状态转换函数:
s 状态下接收 a 转化为 s’,s’ 为一个状态集合
- 可以有多个初态
- 状态转换弧上可以是一个字(或一个正规式)
- 同一个字可能出现在同状态射出的多条弧上(同一状态加入同一个字后可能到达不同的状态)
FA 的等价
L(M) = L(M’),则 M 与 M’ 等价
判定两个自动机等价的算法是存在的
DFA 与 NFA 是等价的,可以将任何 NFA 转化为 DFA
DFA 易于程序实现,NFA 易于人工设计
NFA 的确定化
-
引进新的初态节点 X 和终态节点 Y ,
,从 X 到 中任意状态节点连一条 箭弧,从 F 中所有状态结点连一条 箭弧到 Y (消除了 NFA 和 DFA 在初态和终态上的差别,新的初态只有一个为 X,新的终态只有一个为 Y) -
引入新的状态来拆分字弧线(简化了弧上的字)
如:
,可以转换为 -
子集法:
- 闭包: - closure(I) 为 I 中的所有元素及从 I 中的元素经过任意条 弧所能到达的任何状态 运算 为 经过 弧所能到达的所有状态,再取闭包则为 ,也就是 中的状态经过 1 条 弧和若干条 弧所能到达的状态集合即为 创建矩阵(X 为转化后的初态)假设
- closure({X}) 相同的
只在第一列出现一次,空集也需要放到 中,最多会有 行 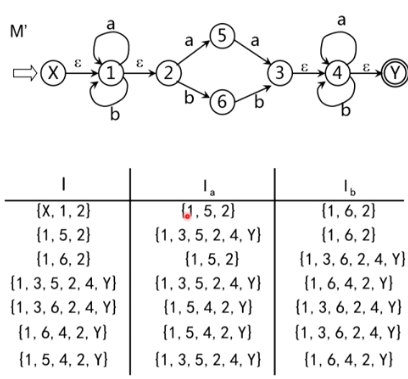
将表视为状态转换矩阵,子集视为状态并编号。初态是
DFA 的化简
状态等价
若两个状态其中一个识别指定字后停留在终态,则另一状态也应如此,反之亦然。
状态可区别
存在某个字,两个状态的其中一个识别后停止于终态,另一个状态没有停止于终态。
状态集划分
划分目标:不相交的子集,两个子集之间是可区别的,而子集内是等价的
- 按照终态与非终态确定初始划分(
字可以区分它们 ) - 假设划分为
,检查 中的每个子集,如果出现 其中的元素包含在现行划分的 N 个不同的子集中,则需要将 划分开来,按照其落入的集合划分。 - 若子集中包含初态,则选为初态,若包含终态,则选为终态。
- 每个子集选择一个代表代表这个子集中的所有状态,所有射向这个子集的元素的箭弧都射向代表,反之亦然
正规式与 FA 的等价
对任何正规式 r,都存在一个 FA M,是的 L(M) = L®
FA 构造正规式
-
添加初态 X 和终态 Y
-
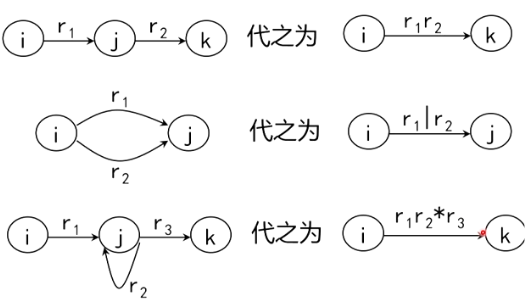
用以上三条规则不断地执行,消除弧和节点,直到只剩下 X 和 Y
正规式构造 FA
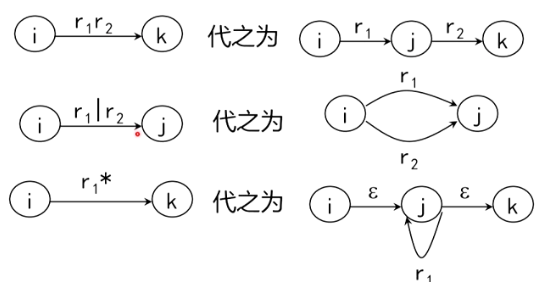
直到弧上都是字符或空字