编译原理：高级语言形式化

文法

描述语言的语法结构的形式规则

字母表（$\sum$）：

• 集合
• 非空
• 有穷

符号：字母表中的元素

符号串（字）：符号构成的一个有穷序列

空字 $\epsilon$：不包含任何符号的序列

$\phi$：不含任何元素的空集

闭包

集合 $\mathrm{\Sigma }$ 的闭包 ${\mathrm{\Sigma }}^{\ast }$ 与正闭包 ${\mathrm{\Sigma }}^{+}$ ，基于字母表 $\mathrm{\Sigma }$ 的全体符号串

设 $\mathrm{\Sigma }=\{a,b\}$ 则：

• 正规闭包：${\mathrm{\Sigma }}^{+}=a,b,aa,ab,ba,bb,aaa,...$
• 闭包：${\mathrm{\Sigma }}^{\ast }={\mathrm{\Sigma }}^{+}\cup \{\epsilon \}$

如果 $\mathrm{\Sigma }$ 原来没空字，则正规闭包中没有空字

上下文无关文法

$$G=(V_T,V_N,S,P)$$

$V_T$ 终结符（非空），$V_N$ 非终结符（非空），$V_T\cap V_N=\varphi$，$S$ 文法的开始符号，$P$ 产生式集合（有限）

产生式

$$P\to \alpha$$

$P\in V_N$, $\alpha \in (V_T\cup V_N{)}^{\ast }$（也就是由终结符和非终结符组成的任意字符串）

产生式表达的是从非终结符转化终结符

设 S 为开始符号，S 必须在某个产生式的左部出现一次

注意：上下文无关文法的产生式的左边为 单个 非终结符

BNF

$$P\to {\alpha }_1|{\alpha }_2|{\alpha }_3|...$$

推导

若存在产生式

$$A\to \gamma$$

则满足：

$$\alpha A\beta \Rightarrow \alpha \gamma \beta$$

$\to$ 代表定义，$\Rightarrow$ 代表直接推出\Rigtarrow

如果

$${\alpha }_1\Rightarrow {\alpha }_2\Rightarrow {\alpha }_3\Rightarrow {\alpha }_4\Rightarrow ...\Rightarrow {\alpha }_n$$

则称 ${\alpha }_1$ 可以推导出 ${\alpha }_n$。其中每一次变化都是直接推出

基于文法 G 的语言 L(G)

$$L(G)=\{\alpha |S\stackrel{+}{\Rightarrow }\alpha ,\alpha \in V_T^{\ast }\}$$

$\stackrel{+}{\Rightarrow }$ 代表可以从 S 开始经过一步或多步($\ge 1$)推导出

$\stackrel{\ast }{\Rightarrow }$ 代表可以从 S 开始经过0步或多步($\ge 0$)推导出

最左推导：任何一步 $\alpha \Rightarrow \beta$ 都是对 $\alpha$ 中的最左非终结符进行替换

最右推导：任何一步 $\alpha \Rightarrow \beta$ 都是对 $\alpha$ 中的最右非终结符进行替换

句子、句型、短句、直接短句、句柄

$$\begin{gathered} G=(V_T,V_N,P,S) \\ S\stackrel{\ast }{\Rightarrow }\alpha A\gamma \end{gathered}$$

若$S\stackrel{\ast }{\Rightarrow }B$ ，则称 B 为一个句型 （就是可以由开始符号推出来的任意串包括开始符号本身）

仅含终结符号的句型为句子 （就是可以由开始符号推出，且只有终结符号）

若 $A\stackrel{+}{\Rightarrow }\beta$，则 $\beta$ 是句型 $\alpha \beta \gamma$ 相对于非终结符 A 的短语

若 $A\Rightarrow \beta$，则 $\beta$ 为直接短语

句柄：一个句型的最左直接短语

归约

推导的逆过程

$$\begin{gathered} \alpha \Rightarrow \beta \\ \beta \stackrel{.}{\Rightarrow }\alpha \end{gathered}$$

• 最左规约
• 最右规约

语法树与二义性

用一张图表示一个句型的推导，这张图称为语法树，也称为推导树

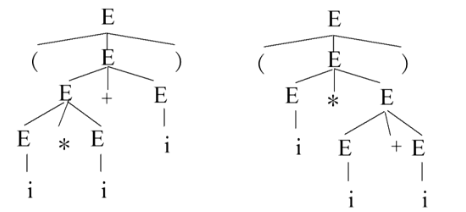
二义性：文法存在某个句子对应两棵不同的语法树

• 无法在有限时间内判断是否具有二义性
• 有判断无二义性的充分非必要条件

若一个文法无二义性，对一个句型的多种推导，采用的各种推导过程，画出来的语法树是一样的。语法树并没有描述具体的推导过程，是不同推导过程的抽象共性。

子树：语法树中的一个节点及其 全部 后裔

短语：子树末端形成的符号串

直接短语：简单子树（只有二级）末端形成的符号串

句柄：位于最左边的简单子树的所有叶节点自左向右排列

乔姆斯基对语言的分类

$$G=(V_T,V_N,S,P)$$

产生式形如：

$$\alpha \to \beta$$

0 型

$$\alpha ,\beta \in (V_T\cup V_N{)}^{\ast }$$

且 $\alpha$ 至少含有一个非终结符号

1 型 （上下文有关）

$$|\alpha |\le |\beta |，\mathrm{仅}S\to \epsilon \mathrm{例}\mathrm{外}$$

2型（上下文无关）

$$\begin{gathered} A\to \beta \\ A\in V_N;\beta \in (V_T\cup V_N{)}^{\ast } \end{gathered}$$

3 型（正规文法、有限自动机）

右线性文法：

$$\begin{gathered} A\to \alpha B\text{or}A\to \alpha \\ \alpha \in V_T^{\ast };A,B\in V_N \end{gathered}$$

左线性文法：

$$\begin{gathered} A\to B\alpha \text{or}A\to \alpha \\ \alpha \in V_T^{\ast };A,B\in V_N \end{gathered}$$

总结

0 型只要求产生式左边包含非终结符

1 型还要求左边的长度要小于右边的长度

2 要求左边只能由一个非终结符组成

3 型要求右边如果有非终结符，只能出现在最左或最右