算法刷题笔记:动态规划
刷题笔记越来越多,导致文档非常臃肿,不便查看,故将动态规划单独拿出来整理
基本技巧
DP 数组初始化
数组多开一行一列,让下标从 1 开始,同时将数组初始化为 0 或 0x7cffff,避免判断边界情况
基本流程
- 确定递推公式、递推次序
- 确定行和列分别代表什么
- 背包问题:物品列表为 1~i 、背包限重为 j 时的最大价值
- 红牌问题(政府服务):如果第 i 步交给第 j 组做,则完成 1~i 步所需的最小时间
- 确定边界值:
- 注意枚举的顺序,有时候应该顺序有的时候应该逆序,主要看问题分析的复杂度主要在谁那,还需要看递推公式的依赖是否已经计算:
- 背包问题:物品列表必须顺序递增,才能逐步增大问题规模,背包限重则顺序逆序都可以
- 红牌问题:步骤从第一步开始,组别从第 2 组开始,最后再处理第一组
- 确定行和列分别代表什么
- 写代码
确定递推次序
难以确定递推次序的通常是需要用记忆化搜索、如果强行寻找 dp 方法可能陷入思路错误或方法更为复杂
- 回文串的递推次序:从回文串的长度入手,长度递增,开始的位置从左往右
滚动数组
当 dp[i][j] 由 dp[i-1][j-n] 决定时,可以只用一个一维数组,注意对 j 的遍历应该从后往前,因为只需要用到 j 自身或前面的,所以后面的可以直接覆盖。
拓扑排序
常见任务
计算有向图中从起点到终点的路径数
- 计算满足指定偏序的排序数
存在的动态规划思想
A 入度为 0 而被清除时, A 指向的节点的路径数 += A 的路劲数
1 | A -> B A 出队列时:num[B] += num[A] |
代码如下
1 | queue<int> q; |
由于是计算路径数,也可以使用记忆化 DFS,但是递归带来的栈空间消耗更大。
背包问题
背包问题本身就是在先确定很小规模的情况下问题的解,然后再逐步扩大物品列表和限重的规模,形成递推
01 背包
01背包问题物品都只有一个,故只用决定放或不放,不用决定放多少
两个因素,一个是物品列表,一个是背包限重,要想到用这两个因素构建矩阵,形成递推式
数组 dp[i][j] 表示从前 i 件物品中选择后装入限重为 j 的背包获得的最大价值
-
第一行均 0:一件物品都无,当然价值为 0
-
在决定限重为 j 的情况下第 i 件物品是否应该装入时,即确定
dp[i][j]:-
j 最小值为
w[i],再小的话完全无法装入第 i 件物品,已经与第 i 件物品没有关系了,故 j 的遍历从w[i]开始 -
若选择装入第 i 件物品,则
dp[i][j] = dp[i-1][j-w[i]] + v[i]因为
dp[i][j]代表此刻背包限重为j,若要装入则需要保证背包还剩余w[i]的限重,故选择用dp[i-1][j-w[i]]时的最大价值加上v[i]来作为装入 i 后的最大价值。需要注意的是,限重较大的最大价值肯定大于等于限重较小的最大价值,故我们计算的时候只需要让剩余的限重刚刚好装入 i 即可。
-
若选择不装第 i 件物品,则
dp[i][j] = dp[i-1][j]因为如果不装,此刻无需腾背包空间,此时最大价值就是尽量都装满前面的 i - 1 个物品,于是就是
dp[i-1][j]
-
-
综上
1
dp[i][j] = max(dp[i-1][j-w[i]] + v[i], dp[i-1][j])
完全背包
完全背包就是同一个物品有无限多个,此时还要考虑同一个物品要放多少个。
dp[i][j] 和 01 背包问题一致,但是在决定装入第 i 件物品的情况下会有所不同,因为可以装入多个,所以应该由 dp[i][j-w[i]] + v[i] 来计算 j 配重下装入 i 的最大价值:
-
为什么不用考虑
dp[i-1][j-w[i]]?dp[i][j-w[i]]一定是大于等于dp[i-1][j-w[i]]的,因为物品的选择多了,但是配重没有改变,在有更有选择的前提下它只可能装价值更多的东西而不可能装更少的东西。
综上:
1 | dp[i][j] = max(dp[i][j-w[i]] + v[i], dp[i-1][j]) |
多重背包
物品数量为有限个,转化为 01 背包问题,把所有物品独立看待,看成只有一个,然后用 01 背包求解
完全背包、多重背包从考虑装入物品的数目出发
1 | dp[i][j] = max{(dp[i-1][j − k*w[i]] + k*v[i]) for every k} |
就是在判断时不只是简单的装与不装之间的 max,而是装入数量从 0 到 k 之间的 max,装 k 个 i 物品时最大价值为 dp[i-1][j − k*w[i]],也就是腾出 k*w[i] 个配重,不装的时候 k = 0 即为dp[i-1][j]
其它问题转化为背包问题
最大约数和:选取和不超过
的若干个不同的正整数,使得所有数的约数(不含它本身)之和最大。
$ A + B + … \leq S
在一堆数里面,拿出一部分数,要求这部分数的和要小于但尽量接近全部和的一半
具体题目:左右脑做题,只要左右脑用时均接近于所有题目的总时长的一半,那所耗费的时间是最少的
背包限重为全部和的一半,每个数看成一个物品,物品重量和价值就是这个数的数值,这样可以保证数相加的和不超过总和的一半(背包限重),也可以保证数相加的和尽可能大(最大价值)
不选也有好处的背包问题
在不选某件物品时也能得到价值的背包问题中,不能只对大于 w[i] 计算,要先计算限重范围在
dp[i][j] 用于表示末尾
dp[i][j] 用于表示末尾:
- 子序列的最后一位
- 挖地牢问题的最后一个地窖
- 最长公共子序列:
dp[i][j]表示字符串 a 前 i 位和字符串 b 前 j 位的最长公共子序列
最长上升子序列 LIS O(n^2)
1 | for (int i = 1; i <= n; i ++) { |
最长上升子序列 LIS O(nlogn)
O(nlogn) 解法:dp[i] 用于表示长度为 i 的上升子序列的末尾最小元素,显然 dp 数组是有序非递减的:
1 | // 扫描 a[i] |
最长不增子序列 O(nlogn) 解法
1 | // dp[i] 存储长度为 i 的最大末尾元素,随着 i 的增加,最大末尾元素一定会减小,故 dp[i] 是一个单调递减的有序序列 |
最长公共子序列 LCS
1 | // 考虑继承 |
可以转化为 LIS 的情况:当 A 和 B 的组成元素相同时,把 A 中的元素根据其位置看做是元素之间的偏序关系,即 A 肯定是一个上升序列,此时就能得出只要是上升的,就都是 A 的子序列,所以只要求 B 的最长上升子序列就可以了。
回文串
计算字符串中的所有回文串
dp[i][j] 表示字符串第 i 位到第 j 位是不是回文串
从 0 开始计数比较方便,且 dp[i][j] 计算结果为上三角矩阵
1 | // 长度为 1 时肯定是回文串 |
不相交的两个回文串组合数
思路:在计算所有回文串的同时
- 计算出以第 i 个字符开头的回文串的数量,存在 begin[i] 中
- 计算所有回文串的末尾元素的下标,存在
vector end中
在计算完成后,计算 begin[i] 的后缀和,此时 begin[i] 代表的是以 i 或 i 之后的字符开头的字符串的数量。
遍历 end 数组,取出 i,显然 i 是一个回文串的末尾元素在字符串中的下标,那这个回文串可以组合的不相交回文串的数量即为 begin[i+1],即 i 之后的字符开头的所有回文串,都能依次和当前的回文串组合,且能保证不相交。
多维 DP
方块取数问题
要求找到两条路径,使得这两条路径经过的方块的值之和最大,被一条路径经过的格子数值会变成 0。
dp[i][j][k][l] 表示第一条路径走到 i j,第二条路径走到 k l 的时候
易错:不能先求一条路径使其最大,再求另一条最大的
1 | // 都取上 一上一左 一左一上 都取左 |
传纸条
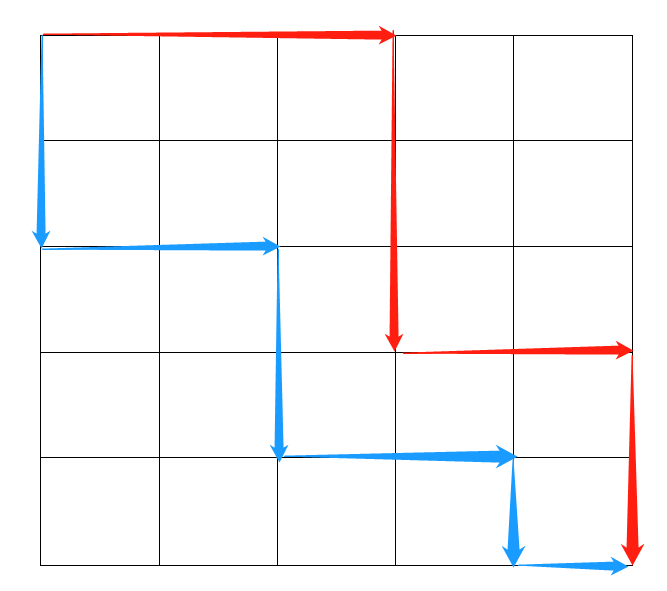
思维转换:不考虑对向,直接找同向的两条路径即可
对于 m*n 的矩阵,不相交的两种处理方式:
-
在所有值均为正的情况下,由于只求值不求路径,即便是 i == k && j == l 的情况下也只需要减去一次
grid[i][j]即可,此时代码和方块取数一样; -
由于两条不相交的路径一定是一上一下、一左一右的,如图所示,可知蓝色路径的行总是大于红色路径,蓝色路径的列总是小于红色路径,所以枚举时 k 从 i + 1 枚举到 m,l 则从 1 枚举到 j - 1,最终状态为
dp[m-1][n][m][n-1]