因果公平分析入门

发表于 2023-08-06 分类于可信人工智能，公平性本文字数： 3.7k

参考资料：Causal Fairness Analysis (causalai.net)

因果基础知识

SCM

Strutural Causal Model

M = ⟨ V, U, F, P (u) ⟩

V: 内层（endogenous, 观测到的）变量的集合，注意这其中就包含了模型的输出 $Y$
U: 外层（exogenous, background）变量的集合。外层变量决定了不同的样本，所以用小写 u 来表示一个确定的样本。
$F$ : 决定 V 的函数集合。 $v_{i} \larr f_{i} (pa (v_{i}), u_{i})$ ，pa(v_i) 表示的是 V 在图中的祖先的取值， $u_{i}$ 则是影响 V 的外层变量的取值。
P(u): 的是 U 的分布

一些表示：

Naturally, their randomness (encoded in P(u)) induces variations in the endogenous set V .

外层变量的随机性导致了 V 的变化，这种随机性使用 P(u) 来表示。
These causal processes – or mechanisms – are assumed to be invariant unless explicitly intervened on

如果不添加显式的干扰，则假定因果机制不会发生变化。
注意 SCM 拥有显式的关于因果机制的定义、内层变量、外层变量以及外层变量的分布。

Submodel

若 X 是 V 的子集，且 x 表示 X 的特定取值，那子模型（Submodel） $M_{x}$ 可以表示为：

M_{x} = ⟨ V, U, F_{x}, P (u) ⟩

$F_{x}$ 表示的是固定住 $X = x$ 后的因果函数，公式表达为：
$F_{x} = {f_{i} : V_{i} \notin X} \cup {X \larr x}$
也可以表述为将所有与 X 有关的公式都替换为 X=x

In words, the SCM $M_{x}$ is obtained from M by replacing all equations in F related to variables X by equations that set X to a specific value x.

一些表示：

In the context of Causal Fairness Analysis, we might be interested in submodels in which the protected attribute X is set to a fixed value x.

Submodel 的使用意义就在于观测某个属性等于一个固定值的情况。

Potential Response

和 Submodel 密不可分的概念。

令 X 和 Y 作为 V 中的两个子集， Potential Response $Y_{x} (u)$ 是子模型 $M_{x}$ 在 $U = u$ 的结果。实际上， $U = u$ 被确定了，即为是一个具体的样本（文中称为 unit）。

Potential Response 也可以写做 Potential outcomes

比如在反事实中，对于同样的一个 $U = u$ ，我们可能会想看 $X = x_{1}$ 和 $X = x_{2}$ 时的情况，也就观测 $Y_{x_{1}} (u)$ 和 $Y_{x_{2}} (u)$

注意，在不指定 U 的时候，Potential Resposne 是一个函数如 $Y_{x}$ 或 $Z_{w}$ 或是其它，表示的是子模型推测 Y 或 Z 的结果。

Observational Distribution

SCM 可诱导（induce）出观测分布。

补充一下概率论的知识：

概率质量函数：Probability mass function，有时也称作离散密度函数，其表示的是离散随机变量每个取值的概率。与概率密度函数不同的是，概率密度函数本身并不是概率，其积分才是概率。而概率质量函数本身的概率，是离散随机变量在各特定取值上的概率。

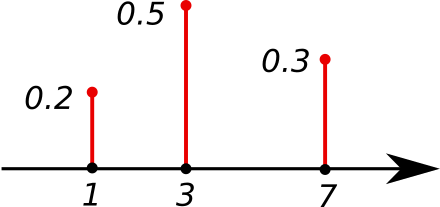
总变差：Total Variation，函数的数值变化的差的总和。如下图，绿色点遍历整个函数后，红色点走过的路程即为总变差。在函数为概率质量函数 $Y = P (X), x \in [x_{0}, x_{1}]$ 的时候，若总变差可以计算为 $P (y | x_{1}) - P (y | x_{0})$ ，由贝叶斯法则，可以进一步拆解为 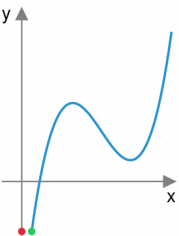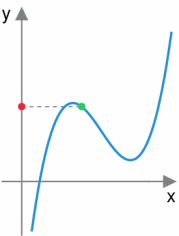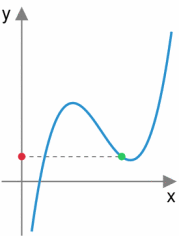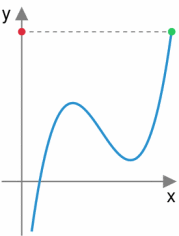$\frac{P (y, x_{1})}{P (x_{1})} - \frac{P (y, x_{0})}{P (x_{0})}$

一个 SCM 诱导了一个联合分布 $P (v_{1}, v_{2}, . . ., v_{n})$ ，对于 V 的每个子集 Y（通常我们将 Y 作为模型的输出，但模型的输出也是 V 的子集没错），Y 的分布可以表示为：

P^{M} (y) = \sum_{u} 1 (Y (u) = y) P (u)

$1 (\cdot)$ 是一个指示函数，当括号内的条件满足时为 1，否则为 0
$Y (u)$ 表示的是在确定 $U = u$ 后，通过因果机制计算的 $K$ 的值。
$P (u)$ 表示的是概率质量函数 $P (U = u)$

式子的意思就是对于每个导致 $Y = y$ 的 $U = u$ ，将它们的概率累加起来。也就是 Y 的分布 P(y)，实际上是由 U 的分布 P(U) 决定的。

the probability mass P(U = u) is accumulated for each instantiation U = u consistent with the event Y = y.

为什么明明 Y 只是 V 的子集，为什么不考虑 V \ Y 中的元素对 Y 的影响？

猜测：作者讨论的是仅仅由 Y 作为内层变量，也就是在分析的时候，不考虑 V \ Y 的因素，或者是将他们固定。

在入学的例子中，Y = {性别, 录取结果}，可想而知，若要判断入学模型是否包含性别歧视，可以分析 P({男, 录取}) 与 P({女, 录取}) ，从他们的总变差来讨论。此时的 P(u) 即为样本集合中各种各样的人的分布。

Counterfactual Distributions

SCM 可诱导（induce）出反事实分布。

反事实分布。（2022 年提出的概念，比较新，可以注意一下）

若 $X, Y, W, Z$ 均是 $V$ 的子集， $Y_{x}, \dots, Z_{w}$ 表示的是各种反事实的事件，也就是 $Y_{x}$ 是 $X$ 取反事实的时候 $Y$ 的输出， $Z_{x}$ 也是同理。

一个 SCM 上有很多个节点，我们可以让其中一些结点取反事实，记作 A（取不同的结点是一种不同的 A，同样的结点取不同的反事实值也是一种不同的 A），此时 SCM 变成了 Submodel。
观察其它一些结点，记作 B，观测 B 的情况，也就是 potential outcome。
在图中取多个 A 和多个 B，每一次这样取 A 和 B，都是一种不同的反事实情况，这就是 $Y_{x}, \dots, Z_{w}$ 所表示的意思。

因此，SCM 诱导了反事实联合分布（就是取不同的 $A_{1}, A_{2}, \dots, A_{n}$ 和 $B_{1}, B_{2}, \dots, B_{n}$ ，随机变量 $S_{1} = ⟨ A_{1}, B_{1} ⟩$ ， $S_{2} = ⟨ A_{2}, B_{2} ⟩$ ，… 的联合分布，注意 $A_{i} \cup B_{i} \sube V$ ）：

P^{M} (y_{x}, \dots, z_{w}) = \sum_{u} 1 (Y_{x} (u) = y, \dots, Z_{w} (u) = z) P (u)

需要注意的是，我们永远都不可能获得真正的反事实分布。

One significant result in this context is known as the causal hierarchy theorem (CHT, for short), which says that it is almost never possible (in an information-theoretic sense) to recover the counterfactual distribution from the observational distribution alone

Casual Diagram

因果图，常用 $G$ 表示

对于每一个 $V_{i} \in V$ ，在因果图中都有一个节点
如果 $V_{i}$ 是 $f_{j}$ 的参数，则存在一个边 $V_{i} \rarr V_{j}$
如果 $U_{i}$ 和 $U_{j}$ 相关（correlated）或 $f_{i}$ 和 $f_{j}$ 共享某些参数 $U_{i j} \in U$ ，则存在变 $V_{i} ⇠⇢ V_{j}$
1
V_i \dashleftarrow\dashrightarrow V_j

一些表述：

there is an edge from an endogenous variable Vi to Vj whenever Vj “listens to” Vi for determining its value.

当 Vj 需要 Vi 来决定它的值的时候，则存在 Vi 到 Vj 的边。
the existence of a bidirected edge between Vi and Vj indicates there is some shared, unobserved information affecting how both Vi and Vj obtain their values.

双向边意味着 Vi 和 Vj 共享一些影响着它们的取值的未观测的信息。
the causal diagram, on the other hand, encodes information only about which functional arguments were possibly used as inputs to the functions in $F$

因果图编码的是因果机制集合 $F$ 的函数的可能的输入。
因果图中出现的 $V_{i} \rarr V_{j}$ ，仅仅表明 $V_{i}$ 可能作为 $f_{j}$ 的参数，对于一个实例， $f_{i}$ 可能会不考虑 $V_{i}$ 的值。

但是因果图中不出现边，则代表着这两个内层变量没有任何关系，这是确定的，在任何情况下都不会成为另一方的函数参数。

所以在确定因果图的时候，应该尽可能地确定更多的因果关系。

SFM

Standard Fairness Model，标准公平性模型。

SFM 的因果图 $G_{S F M}$ ，含有内层变量组 ${X, Z, W, Y}$ ，如下所示：

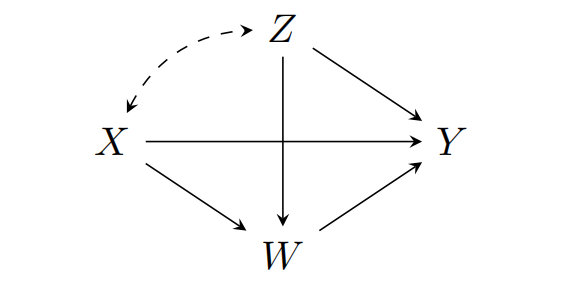
X: protected
Z: confounding，对 X 有影响，但不是通过因果机制影响的
W: mediator，有可能会被通过因果影响的
Y: outcome

将一个普通的因果图 $G$ 投影到 SFM，就是将 $G$ 中的 V 映射到如上的四个组中，这个过程用 $Π_{S F M} (G)$ 表示。

上述过程也叫 Standardize

SFM 的特点：

SFM 中并没有考虑 Z 和 W 中的变量之间的因果关系；
SFM 基于不同变量组之间不存在 confounding 的假设，也就是图中除了 X 和 Z 之间外，没有其它双向箭头。

因果公平基础知识

结构化公平判断准则

Structural direct criterion：要求的是 X 不为 Y 的父节点，也就是不直接影响 Y
${Str-DE}_{X} (Y) = 1 (X \in pa (Y))$
Structual indirect criterion: 要求的是 X 不为 Y 的祖先结点，也就是不间接影响 Y
${Str-IE}_{X} (Y) = 1 (X \in an (pa (Y)))$
Structual spurious criterion: 要求的是参与决定 X 的变量不参与决定 Y
${Str-DE}_{X} (Y) = 1 ((U_{X} \cap an (Y) \neq \empty) \lor (an (X) \cap {an}_{G_{\underset{―}{X}}} (Y) \neq \empty))$
其中 $G_{\underset{―}{X}}$ 表示的是从因果图 $G$ 中去掉所有从 X 出发的边。

the structural spurious criterion verififies whether there exist variables that both causally affect the attribute X and the outcome .

以上准则都是公式结果为 0 时代表符合该准则，反之则为不符合。

公平性度量

Admissibility: 若一个公平性度量 $μ$ 对于某个公平性准则 $Q$ 是可接受（admissible）的，则表明 $Q (M) = 0 \rarr μ (M) = 0$

A measure µ is said to be admissible w.r.t. the structural criterion Q within the class of models Ω, or (Q, Ω)- admissible

TV is not admissible w.r.t. Str-DE, IE, SE, but it is decomposable.
Decomposability: 可分解性，若一个度量 $μ$ 是可分解的，则表明存在其它度量 $μ_{1}, μ_{2}, \dots, μ_{k}$ 可使得 $μ = f (μ_{1}, \dots, μ_{k})$ 成立。

因果公平分析的基本问题

$Q_{1}, \dots, Q_{k}$ 是一系列因果公平准则
$μ$ 是个公平性度量

因果公平分析的基本问题（The Fundamental Problem of Causal Fairness Analysis, FPCFA）就是：

找到一些列的 $μ_{1}, μ_{2}, \dots, μ_{k}$ ，使得 $μ$ 可分解为 $μ_{1}, μ_{2}, \dots, μ_{k}$
$μ_{1}, μ_{2}, \dots, μ_{k}$ 对于 $Q_{1}, \dots, Q_{k}$ 是可接受的

如果可以完成以上工作，则可以证明这个该因果机制是公平的

这同时是性质上、数值上的操作， $μ_{i}$ 本身的数值是数值上的， $μ_{i}$ 所代表的实际意义则是性质上的。

事实与反事实偏差

偏差（Variation）的个人理解：偏差就是模型的结果在某些指标上对不同的人群存在明显的差异。比如 P(Y=1| X=男) 和 P(Y=1| X=女) 这两个数值可能存在较大的差异，但是从辛普森悖论来说，单单从这个指标上来看并不能就此确定模型时不公平的。要把它标准化为因果公平分析的基本问题来解决。

Factual & Counterfactual Variations

Contrast $C$

C (C_{0}, C_{1}, E_{0}, E_{1}) = E [y_{C_{1}} | E_{1}] - E [y_{C_{0}} | E_{0}]

$E_{0}, E_{1}$ 是观测到的事实情况（含有多种情况/事件）
$C_{0}, C_{1}$ 是施加的干预
上面的式子就是对经历 $E_{0}$ 事件的个体，施加 $C_{0}$ 干预，然后观察其输出 $y_{C_{0}}$ ，并将其与 $y_{C 1}$ 做比较

当

$E_{0} = E_{1}$ ，则 Contrast 被称为是反事实的。

就是使得个体经历相同的事件，但是对其值施加不同的影响，来观察其变化
$C_{0} = C_{1}$ ，则 Contrast 称为是事实的。

就是使个体经历不同的事件，但对其值施加相同的影响，来观察其变化

在只考虑二元的情况下，也就是上面的 $[y_{C_{1}} | E_{1}]$ 和 $[y_{C_{0}} | E_{0}]$ 中 $y$ 是二元离散值。Contrast 可写作

P (y_{C_{1}} | E_{1}) - P (y_{C_{0}} | E_{0})

上式可分解为反事实 contrast 与事实 contrast

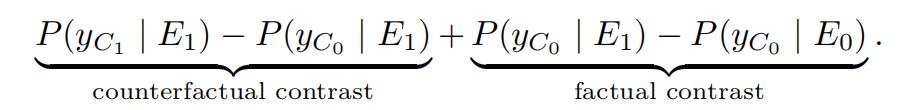
Counterfactual contrast ( $C_{c t f}$ )，也就是 $E_{0} = E_{1} = E$ 的时候，可以计算为

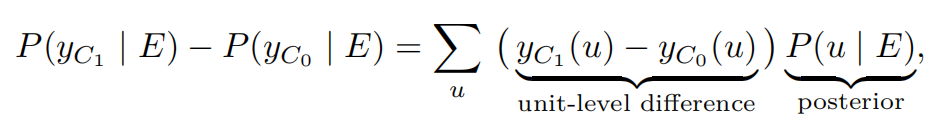
上述式子将 contrast 和结构化因果模型建立了基本的联系，因为正如前文所述，SCM 本身可诱导出事实分布与反事实分布，与上式中的分布可以相对应。

下面用二段式生成过程（two-step generative process）来解释上面的式子 😄。二段式生成过程：

Sampling: 取样，也就是一个样本 U=u 从分布 P(u) 中取出的过程。
Evaluating: 评估，也就是一个确定的样本 u 通过因果机制影响所有内层变量的过程。

上面的式子中：

$P (u | E)$ 即为取样的过程。 $E$ 代表的是样本经历过的所有事件，也就是限定取样时样本的条件。当 $E = {}$ 时，则样本取样完全随机，当 $E = {X = x, \dots}$ 时，则限定样本需要满足哪些条件。可见，在该式中，对所有样本的限定条件是相同的。
$y_{C_{1}} (u) - y_{C_{0}} (u)$ 表示的即为评估的过程。对因果机制施加两种不同的变化，具体来说就是取 SCM 的两个不同的 SubModel。举例来说，就是将 SCM 中 $X \in V$ 固定为两个不同的值 $C_{0}, C_{1}$ ，然后观测确定的样本 $u$ （注意，只有样本的随机性消失了，也就是样本 $u$ 确定了，才可以通过因果机制）所产生的不同的 $y$ 之间的差别，这种差别是样本级别（unit-level）的
将所有样本的上述过程计算后加起来，即为整个样本集的 Counterfactual contrast。左式即为在不确定 u 的时候的表达方式。
通过上述方法所产生的偏差是通过因果机制产生的，称作 downstream variation。我们可以通过上面的过程，来考量 X 对 Y 的影响。
通过在 E 中添加越来越多的限制，我们可以限定取样的人群，从而更为精细地观察该因果机制在指定人群中产生的作用。

Factual contrast ( $C_{f a c t u a l}$ )，也就是 $C_{0} = C_{1} = C$ 的情况，可以计算为

理解了前面的 Counterfactual contrast，也就不难理解 Factual contrast 了。值得一提的是，factual contrast 所代表的偏差，是 non-causal （spurious）的，也就是其不是通过因果机制产生的偏差。但是其也可以用来考量非因果机制的 X 对 Y 的影响。

可解释平面

Explainability plane

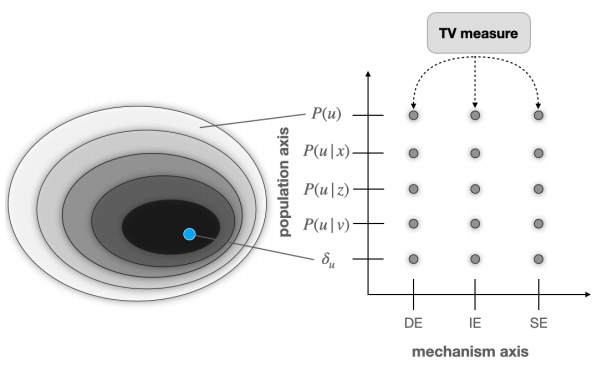
上图中，横轴代表的是不同的因果机制（直接、间接、虚假），纵轴代表的不同的人群。随着人群的越来越精细，可以制定越来越有力的公平措施。