鲁棒性与类间公平性存在 Trade Off

Note

论文题目：To be robust or to be fair: Towards fairness in adversarial training

概论

对抗训练是提高模型对抗鲁棒性最有效和可靠的方法之一。但是，该研究发现对抗训练会导致模型在准确率和鲁棒性上出现很大的类间性能差异（class-wise performance discrepancy），这种差异在自然训练（natural training）中是不会出现的。这种现象即便在平衡的数据集中仍然存在。

这种类间差异对安全性有着很大的威胁，比如交通信号灯的识别如果整体性能很高，但对某种信号的性能很低，那这种识别的安全型还是不能保证的。这种差异从社会伦理的角度上来看也存在着问题。

该研究将这样的类间差异问题定义为鲁棒公平性问题（robust fariness problem）。作者进一步提出了：

• 为什么对抗训练会出现这种类间差异而自然训练不会：因为对抗训练会导致模型更青睐那些易于被分类的样本，而牺牲那些难以被分类的样本的准确度。（只是从分类难度的角度来考虑）
• 提出了 Fair Robust Learning（FRL）来解决鲁棒公平性问题

一些术语：

• 标准性能/误差（standard performance / error）：在干净样本上的性能/错误率
• 鲁棒性能/误差（robust performance / error）：在对抗样本上的性能/错误率

鲁棒公平性问题

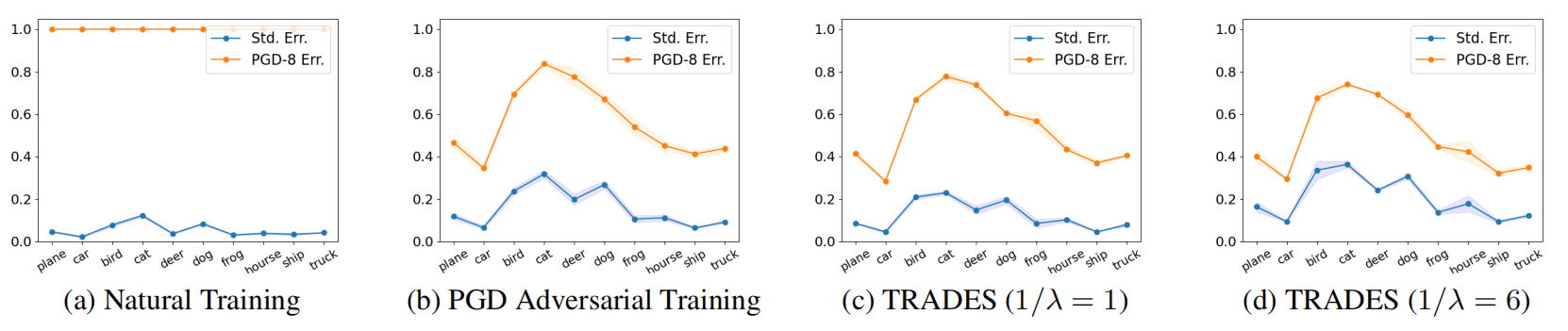
❓ 自然训练下，PGD 的攻击成功率是 100%，从而使得类别间的错误率完全相同，这是否掩盖了在较差的攻击方式下不同类别的错误率可能也存在着差异？

上图是在 CIFAR-10 数据集上的实验结果，蓝色线表示对不同类别的分类错误率，橙色线表现在进行 PGD 攻击时不同类别的分类错误率。可以看到，在进行对抗训练的 b c d 三图中，不同类别之间的错误率存在着较大差异。

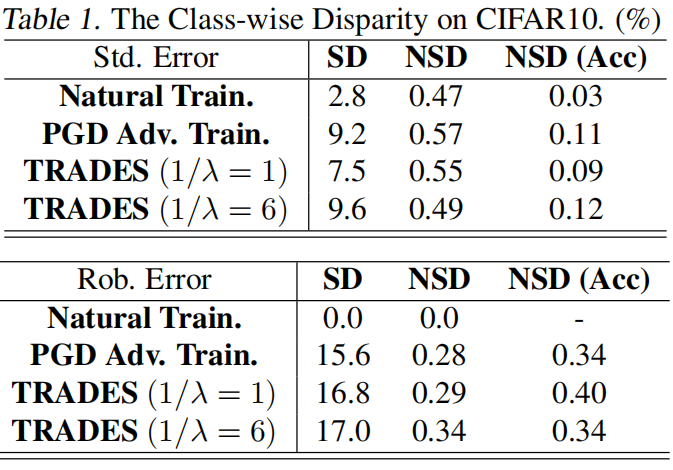
除了折线图的形式，作者还提供 SD、NSD、NSD（Acc）统计数据（Table 1）

1. Standard Deviation of class-wise error (SD)：即各类错误率的标准差：

   $$SD=\sqrt{\frac{1}{N}\sum _{i=1}^N(e_i-\overline{e}{)}^2}$$

   其中 $e_i$ 是第 $i$ 类的错误率，$\overline{e}$ 是所有类别错误率的平均值，$N$ 是类别数。

2. Normalized Standard Deviation of class-wise error (NSD)：对类间错误率标准差进行标准化的结果。标准化的方式可能会根据具体定义而有所不同，一种常见方法是将 SD 除以平均错误率，即：

   $$NSD=\frac{SD}{\overline{e}}$$

   这样可以去掉由于平均错误率大小带来的影响，更关注类别间的相对离散程度。

3. Normalized Standard Deviation of class-wise accuracy (NSD (Acc))：这是对每个类别的准确率进行标准化后的标准差。先求每类的准确率的标准差，然后标准化：

$$NSD(\text{Acc})=\frac{\sqrt{\frac{1}{N}\sum _{i=1}^N(a_i-\overline{a}{)}^2}}{\overline{a}}$$

其中 $a_i$ 是第 $i$ 类的准确率，$\overline{a}$ 是所有类别的平均准确率，$N$ 是类别数。

鲁棒公平性问题的成因

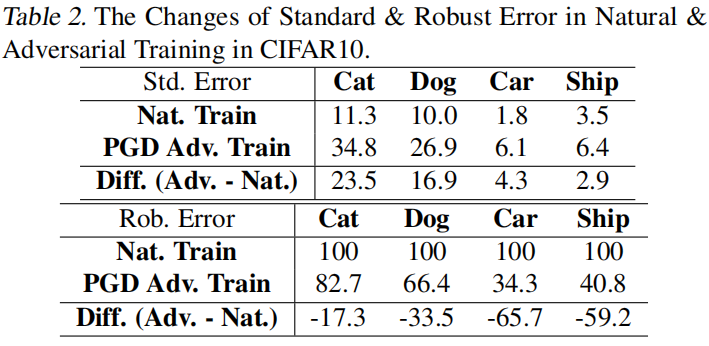
Table2 记录了不同类别的标准&鲁棒错误率，可以看到的是，对于标准错误率较高的类别（猫、狗），其鲁棒错误率也较高，且其鲁棒错误率在对抗训练后的改善相对易于分类的类别来说较少。由此可见，对抗训练可能对原本分类难度较高的类别的投入较少，进而致使类间的性能差异。

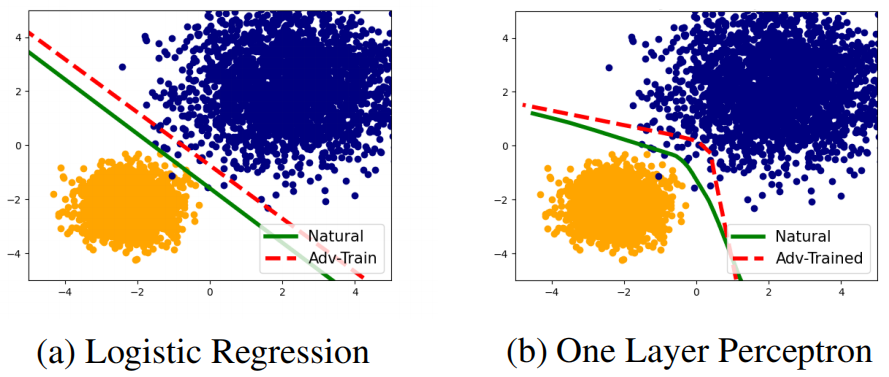
为了进一步证实作者的想法，作者在一个 mixture Gaussian 分布下进行了实验。他们设置了两个不同的类别，他们拥有不同的分类难度，且对抗训练不会显著地降低他们的平均误差，以此来证明对抗训练带来的类间差异并不是准确率降低的自然结果。

具体来说，作者对正类和负类设置了不同的方差 ${\sigma }_{+1}$ 和 ${\sigma }_{-1}$，并且 $\sigma_{+1} : \sigma_{-1} = K:1 $，以此使得正类比负类更加难以分类，因为其数据空间更大（less compacted in the data space），作者在 Theorem 1 中说明了这一点，其证明了一个最优的分类器会在正类上产生较大的标准误差。

$$\begin{array}{r}y{\sim }^{u.a.r}\{-1,+1\},\theta =(\underset{\text{dim}=d}{\underbrace{\eta ,\dots ,\eta }}),\\ x\sim \{\begin{array}{ll}\mathcal{N}(\theta ,{\sigma }_{+1}^{2}I)& \text{if }y=+1\\ \mathcal{N}(-\theta ,{\sigma }_{-1}^{2}I)& \text{if }y=-1\end{array}\end{array}$$

对抗训练后的模型会对这两个类产生不同的性能，因为其决策边界会更靠近正类（蓝色），更远离负类（黄色）。

Theorem 1: 正类拥有更大的标准误差，所以更难分类

Theorem 2: 正负类的类内标准误差受 K 的影响

Corollary 1: 对抗训练后的模型会提高正类的标准误差并降低负类的标准误差

综上，我们可以总结：

1. 对抗训练所带来的类间公平性问题是来自于对抗训练本身；
2. 对抗训练会将决策边界推向更难分类的类；
3. 对抗训练会牺牲更难分类的类的性能，并提高更易于分类的类的性能，进而导致了严重的类间不公平；

鲁棒公平性目标

1. 均衡准确性（Equalized Accuracy）：一个分类器 $f$ 的标准误差在统计上独立于真实标签 $y$：
   $Pr(f(x)\ne y|Y=y)\approx Pr(f(x)\ne y)$ 对于所有 $y\in Y$。

   这方面是统计公平领域所研究的

2. 均衡鲁棒性（Equalized Robustness）：一个分类器 $f$ 的鲁棒误差在统计上独立于真实标签 $y$：
   $Pr(\mathrm{\exists }\parallel \delta \parallel \le ϵ,f(x+\delta )\ne y|Y=y)\approx Pr(\mathrm{\exists }\parallel \delta \parallel \le ϵ,f(x+\delta )\ne y)$ 对于所有 $y\in Y$。

目标是训练一个分类器 $f$ 在拥有最小的总体鲁棒误差的同时，让 $f$ 满足上述的公平约束

$$\begin{array}{rl}& \underset{f}{min}{\mathcal{R}}_{\text{rob}}(f)\\ & \text{s.t.}\{\begin{array}{l}{\mathcal{R}}_{\text{nat}}(f,i)-{\mathcal{R}}_{\text{nat}}(f)\le {\tau }_1\\ {\mathcal{R}}_{\text{rob}}(f,i)-{\mathcal{R}}_{\text{rob}}(f)\le {\tau }_2\text{for each }i\in Y\end{array}\end{array}$$

其中，${\tau }_1$ 和 ${\tau }_2$ 是较小的正数，指可接受的不公平性。约束中约束了每个类别的自然误差和鲁棒误差都不应该大幅超过平均误差。

Fair Robust Learning (FRL)

FRL (Reweight)

由于鲁棒误差往往与标准误差有着强关联，所以对类别 $i$ 的鲁棒误差和标准误差之间可能存在着缠绕的影响。因此，作者借助 TRADES 方法，将鲁棒误差调整为了 standard erro 和 boundary error 的和。其中 ${\mathcal{R}}_{\text{bndy}}$ 表示的是一个 $i$ 类的样本可能靠近决策边界且可以被攻击的概率。

$$\begin{array}{rl}{\mathcal{R}}_{\text{rob}}(f,i)& =Pr\{\mathrm{\exists }\delta ,\text{s.t.}f(x+\delta )\ne y\mid y=i\}\\ & =Pr\{f(x)\ne y\mid y=i\}+Pr\{\mathrm{\exists }\delta ,f(x+\delta )\cdot f(x)\le 0\mid y=i\}\\ & ={\mathcal{R}}_{\text{nat}}(f,i)+{\mathcal{R}}_{\text{bndy}}(f,i)\end{array}$$

在此之后，我们就单独地解决标准误差、边界误差的不公平性，进而解决标准误差和鲁棒误差的不公平性。在优化边界误差时，作者使用的是前人所使用的最小化干净样本和对抗样本的logits之间的KL散度。

$$\begin{array}{rl}& \underset{f}{min}{\mathcal{R}}_{\text{nat}}(f)+{\mathcal{R}}_{\text{bndy}}(f)\\ & \text{s.t.}\{\begin{array}{l}{\mathcal{R}}_{\text{nat}}(f,i)-{\mathcal{R}}_{\text{nat}}(f)\le {\tau }_1\\ {\mathcal{R}}_{\text{bndy}}(f,i)-{\mathcal{R}}_{\text{bndy}}(f)\le {\tau }_2\text{for each }i\in Y\end{array}\end{array}$$

使用拉格朗日乘子法后，可以将约束整合进函数 $L$ 内：

$$\begin{array}{rl}L(f,\varphi )=& {\mathcal{R}}_{\text{nat}}(f)+{\mathcal{R}}_{\text{bndy}}(f)\\ & +\sum _{i=1}^Y{\varphi }_{\text{nat}}^i{({\mathcal{R}}_{\text{nat}}(f,i)-{\mathcal{R}}_{\text{nat}}(f)-{\tau }_1)}^{+}\\ & +\sum _{i=1}^Y{\varphi }_{\text{bndy}}^i{({\mathcal{R}}_{\text{bndy}}(f,i)-{\mathcal{R}}_{\text{bndy}}(f)-{\tau }_2)}^{+}\end{array}$$

进而，问题变为一个 max-min game。

$$\underset{{\varphi }_{\text{nat}},{\varphi }_{\text{rob}}\ge 0}{max}\underset{f}{min}L(f,\varphi )$$

实现上，作者先利用一个预训练的鲁棒模型再来测试其在一个单独的验证集上的标准误差和边界误差。测试当前模型是否违背了上述的约束，如果违背了，其拉格朗日乘子会被调整为对应的值，以提高某个类的训练权重。在固定乘子后，将优化 $f$ 在最小化内层的式子。

FRL (Remargin)

尽管提高特定类别的标准误差损失 ${\mathcal{R}}_{\text{nat}}(f,i)$ 有助于惩罚那些过大的 ${\mathcal{R}}_{\text{nat}}(f,i)$ 来提高性能更差的组的标准表现，然而，单纯提高一个类的边界误差损失可能无法达到降低其边界误差的目的。作者通过在 CIFAR-10 的实验上发现，在使用 PGD 进行对抗训练的时候，即便对某个类别给予很大的边界误差权重，仍然不足以降低其边界误差。

前人的发现指出，提高扰动范围 $ϵ$ 可以有效提高模型针对当前扰动的鲁棒性。因此，如果我们想要降低某个类别 $i$ 的边界误差，我们可以通过提高该类别的对抗样本的扰动范围的方式来进行。该方法被称为 FRL (Remargin)。具体来说，边界误差越大的类别的样本会赋予越大的扰动范围。

$${ϵ}^i={ϵ}^i\cdot \exp ({\alpha }_2^{\ast }({\mathcal{R}}_{\mathrm{bndy}}(f,i)-{\tau }_2)))$$

FRL (Remargin) 可以和 FRL (Reweight) 结合。

实验

Baselines: 两个对抗防御方法、一个公平性方法

Datasets: CIFAR-10、SVHN

Model: PreAct-ResNet18、WRN28

Metirc: Average/Worst Std Error、Average/Worst Robust Error

Conclusion: Remargin+Reweight 效果最好，Rob. 甚至比不考虑公平性的方法要好，因为用了更大的扰动，但是 Std. 降低了，也是因为用了更大的扰动。