Patch-fool: Are vision transformers always robust against adversarial perturbations?

Conclusion

ViT 的对抗鲁棒性并不总高于 CNN

每个 patch 的干扰像素的数量高度影响 ViT 和 CNN 之间的鲁棒性排名

提出了 Patch Fool 方法及其两个变种，总结就是对部分patch、patch 内的部分像素做干扰，在交叉熵损失函数后添加了一项用于提高所选patch对其它patch的注意力值的项

Related work

一些工作指出，在足够数量的数据集上训练的 ViT，在大部分的情况下至少与和它相对应的 ResNet 一样鲁棒，无论是在自然损坏、分布偏移还是对抗性干扰的场景中 [1]。在 $L_p$ 攻击下，ViT 比 CNN 更加鲁棒 [2]。ViT 学习更少的低级特征并且更具有泛化性，使得他们更加鲁棒。如果在 ViT 中加入卷积块，则会降低它的鲁棒性 [3]。

[1] Bhojanapalli S, Chakrabarti A, Glasner D, et al. Understanding robustness of transformers for image classification[C]//Proceedings of the IEEE/CVF international conference on computer vision. 2021: 10231-10241.

[2] Aldahdooh, Ahmed, Wassim Hamidouche, and Olivier Deforges. “Reveal of vision transformers robustness against adversarial attacks.” arXiv preprint arXiv:2106.03734 (2021).

[3] Shao R, Shi Z, Yi J, et al. On the adversarial robustness of vision transformers[J]. arXiv preprint arXiv:2103.15670, 2021.

Patch Fool

Attack setup

符号：

• 由多个 patch 组成的图片 $\mathbf{X}=[{\mathbf{x}}_1,\dots ,{\mathbf{x}}_n{]}^{\mathrm{\top }}\in {\mathbb{R}}^{[n\times d]}$ ，$n$ 是 patch 的数量，$d$ 是每个 patch 的维度
• 对抗性干扰 $\mathbf{E}$
• one hot vector ${\mathbb{1}}_p\in {\mathbb{R}}^n$，只有第 $p$ 个元素是 1
• 损失函数 $J$

攻击的目标是：

$$\underset{1\le p\le n,\mathbf{E}\in {\mathbb{R}}^{n\times d}}{\arg max}J(\mathbf{X}+{\mathbb{1}}_p\odot \mathbf{E},y)$$

其中 $\odot$ 是 penetrating face product，就是用 ${\mathbb{1}}_p$ 乘以 $\mathbf{E}$ 的每个列向量（相同维度下的逐元素相乘）理解：对于每个图片，不止需要确定我们要干扰哪个 patch，而且要确定我们的具体干扰。

根据 Attention 确定 ${\mathbb{1}}_p$

用 $a_j^{(l,h,i)}$ 表示第 $j$ 个 patch 在第 $l$ 层上第 $h$ 个头对第 $i$ 个 patch 的注意力值。用 $s_j^{(l)}$ 表示第 $j$ 个 patch 在第 $l$ 层对其它 patches 的注意力值的总和。在某一层，挑选最大的 $s_j^{(l)}$ 中的 $j$ 作为进行干扰的 patch。

$$s_j^{(l)}=\sum _{h,i}{a}_j^{(l,h,i)}$$

论文中，将 $l$ 设置为 5，因为在后面的层中第 $j$ 个 patch 可能混杂了很多其它 patch 的信息导致其不能代表我们输入时的那个 patch。

Attention-aware Loss

为了最大化选定的 patch 的影响，论文选择用一个损失函数来最大化这个 patch 对其它 patch 的注意力，也就是在 $l$ 层中，我们要最大化以下的损失函数：

$$J_{\text{ATTN }}^{(l)}(\mathbf{X},p)=\sum _{h,i}{a}_p^{(l,h,i)}$$

将上面的损失与最大化分类差距的交叉熵 $J_{\mathrm{CE}}$ 相结合，形成了：

$$J(\tilde{\mathbf{X}},y,p)=J_{\mathrm{CE}}(\tilde{\mathbf{X}},y)+\alpha \sum _l{J}_{\mathrm{ATTN}}^{(l)}(\tilde{\mathbf{X}},p)$$

为了解决这两个损失的梯度冲突，论文使用了 PCGrad 来更新干扰，也就是对于 $\mathbf{E}$ 的梯度 ${\delta }_{\mathbf{E}}$，我们计算其为：

$$\begin{array}{c}{\delta }_{\mathbf{E}}={\mathrm{\nabla }}_{\mathbf{E}}J(\tilde{\mathbf{X}},y,p)-\alpha \sum _l{\beta }_l{\mathrm{\nabla }}_{\mathbf{E}}{J}_{\mathrm{CE}}(\tilde{\mathbf{X}},y)\\ {\beta }_l=\{\begin{array}{cl}0,& ⟨{\mathrm{\nabla }}_{\mathbf{E}}{J}_{\mathrm{CE}}(\tilde{\mathbf{X}},y),{\mathrm{\nabla }}_{\mathbf{E}}{J}_{\mathrm{ATTN}}^{(l)}(\tilde{\mathbf{X}},p)⟩>0\\ \frac{⟨{\mathrm{\nabla }}_{\mathbf{E}}{J}_{\mathrm{CE}}(\tilde{\mathbf{X}},y),{\mathrm{\nabla }}_{\mathbf{E}}{J}_{\text{ATTN }}^{(l)}(\tilde{\mathbf{X}},p)⟩}{{\Vert {\mathrm{\nabla }}_{\mathbf{E}}{J}_{\mathrm{CE}}(\tilde{\mathbf{X}},y)\Vert }^2},& \text{ otherwise }\end{array}\end{array}$$

作者还进一步使用了 Adam 优化器来根据梯度确定更新 $\mathbf{E}$ 的方向

$${\mathbf{E}}^{t+1}={\mathbf{E}}^t+\eta \cdot \mathrm{Adam}\left({\delta }_{{\mathbf{E}}^t}\right)$$

Variant

需要对 patch 中的多少像素做干扰才能可以？

• 只对很少的像素做干扰 （sparse patch fool）
• 对整个 patch 做干扰（前文所述的 patch fool）

Sparse patch fool 使用 mask $\mathbf{M}$ 来决定只对哪些像素做干扰，并把它作为一个可学习的参数，在反向传播的时候，使用直通估计器来更新 $\mathbf{M}$ 中的元素，也就是使用损失对 $(\mathbf{M}\circ \mathbf{E})$ 的梯度作为对 $\mathbf{M}$ 的梯度。

$$\underset{1\le p\le n,\mathbf{E}\in {\mathbb{R}}^{n\times d},\mathbf{M}\in \{0,1{\}}^{n\times d}}{\arg max}J(\mathbf{X}+{\mathbb{1}}_p\odot (\mathbf{M}\circ \mathbf{E}),\text{ y) s.t. }\parallel \mathbf{M}{\parallel }_0\le k$$

MILD Patch-Fool

为了符合 $L_P$ 攻击方法的范式，可以在每次更新 $\mathbf{E}$ 后对其进行缩放（$L_2$） 或 Clip （$L_{\text{infin}}$）

Experiments

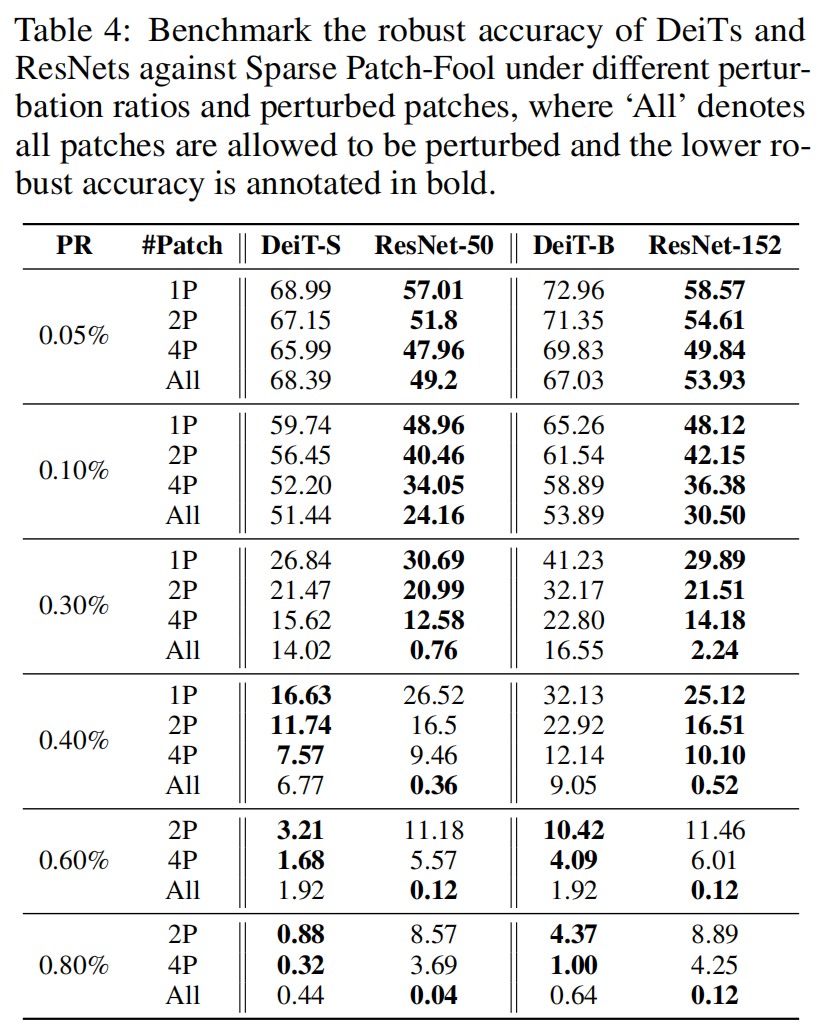
PR 为 patch 内干扰的像素比例，#Patch 为干扰的 patch 数量，指标是鲁班准确率。可以看到 DeiT 和 ResNet 在不同的 PR 和 #Patch 下的鲁棒性会有差异，没有谁恒优于谁。加粗的是比较差的。

下面是 $L_{\text{infin}}$ 的 MILD Patch-Fool 的结果