Improving the adversarial transferability of vision transformers with virtual dense connection

Motivating Study

作者线性地减少 ViT 内各个组件的梯度的影响 （from 1 to 0 swith step size of 0.25）然后看看各个组件对迁移性的影响，得到的结论是消除 skip connection 后可迁移性下降最严重，无论是 Attention 模块还是 MLP 模块的 Connection

作者认为这是因为 skip connection 有助于传播来自 ViT 深层的梯度，而且 ViT 深层又捕获了更高级的特征，所以这些梯度更有助于可迁移性。

VDC

VDC（Virtual Dense Connection）是一种密集连接的方法。从 Motivating Study 的结论中可以看出，skip connection 对可迁移性至关重要。既然如此，我们就可以增加 skip connection 的使用程度，参考 CNN 中的 DenseNet 将每一层与其后的所有层全部连接。

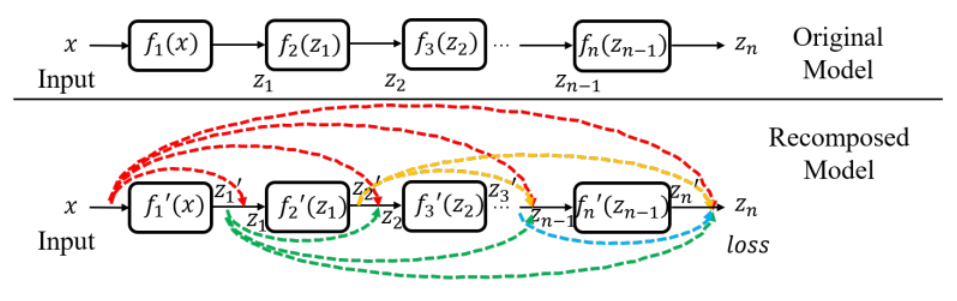
在具体实现上，由于不想改变模型的 forward pass，所以这种密集连接是虚拟存在的，也就是只在计算梯度的时候使用。假设·进行了密集连接，那模型中第 $i$ 个块 $bloc{k}_i$ （可能是 Attention 也可能是 MLP）用数学表示就是：

$$f_i^{\prime }\left({\mathit{z}}_{i-1}\right)=f_i\left({\mathit{z}}_{i-1}\right)-\mathit{x}-\sum _{k=1}^{i-1}{\mathit{z}}_k^{\prime }$$$${\mathit{z}}_{i-1}=\mathit{x}+\sum _{k=1}^{i-1}{\mathit{z}}_k^{\prime }$$

其中 $z_{i-1}^{\prime }$ 是重组后 $bloc{k}_{i-1}$ 的输出，$z_{i-1}$ 是重组后 $bloc{k}_i$ 的输入。由于进行了密集连接，所以 $z_{i-1}^{\prime }\ne z_{i-1}$。 $f_i^{\prime }$ 是密集连接后的块，而 $f_i$ 是原始块。对 $f_i^{\prime }\left({\mathit{z}}_{i-1}\right)$ 进行求导，可以得到其导数 ${\mathit{g}}_i^{\prime }$。

$${\mathit{g}}_i^{\prime }=\frac{\partial f_i^{\prime }\left({\mathit{z}}_{i-1}\right)}{\partial {\mathit{z}}_{i-1}}=\frac{\partial (f_i\left({\mathit{z}}_{i-1}\right)-\mathit{x}-\sum _{k=1}^{i-1}{\mathit{z}}_k^{\prime })}{\partial {\mathit{z}}_{i-1}}=\frac{\partial (f_i\left({\mathit{z}}_{i-1}\right)-{\mathit{z}}_{i-1})}{\partial {\mathit{z}}_{i-1}}={\mathit{g}}_i-\mathbf{1}$$

从 ${\mathit{g}}_i^{\prime }$ 的式子中可以看出，即便我们没有实际地改变模型结构进行 skip connection，我们也能够计算出如果进行了 skip connection，其梯度会是怎么样的，因为这其中只用到了 ${\mathit{g}}_i$。在计算出 ${\mathit{g}}_i^{\prime }$ 后，我们便可以通过链式法则，逐步计算出在 dense connect 的情况下损失函数对输入的梯度 $\text{Grad}$：

$$\begin{array}{rl}\text{ Grad }& =\frac{\partial \text{ loss }}{\partial {\mathit{z}}_n}\prod _{k=1}^n(\lambda {\mathit{g}}_k^{\prime }+\mathbf{1})=\frac{\partial \text{ loss }}{\partial {\mathit{z}}_n}\prod _{k=1}^n(\lambda ({\mathit{g}}_k-\mathbf{1})+\mathbf{1})\\ & =\frac{\partial \text{ loss }}{\partial {\mathit{z}}_n}\prod _{k=1}^n(\lambda {\mathit{g}}_k+(1-\lambda )\mathbf{1}).\end{array}$$

令 $\gamma =\frac{1-\lambda }{\lambda }$，我们可以进一步简化 $\text{Grad}$ 为：

$$\text{ Grad }=\frac{\partial \text{ loss }}{\partial {\mathit{z}}_n}\prod _{k=1}^n({\mathit{g}}_k+\gamma \mathbf{1})$$

然而，这样的计算方法是不高效的，为了解决这个问题，作者提出了 consecutive skip assumption。具体来说，就是在计算 $\text{Grad}$ 时，将 $\frac{\partial \text{ loss }}{\partial {\mathit{z}}_n}\prod _{k=1}^n({\mathit{g}}_k+\gamma \mathbf{1})$ 式子展开成很多项，然后通过删除一些项作为近似，计算结果为：

$${\text{ ConGrad }}_i={\mathrm{Grad}}_i+s\cdot \sum _{j=i+1}^n{\mathrm{Grad}}_j\cdot {\gamma }^{n-j+1}$$