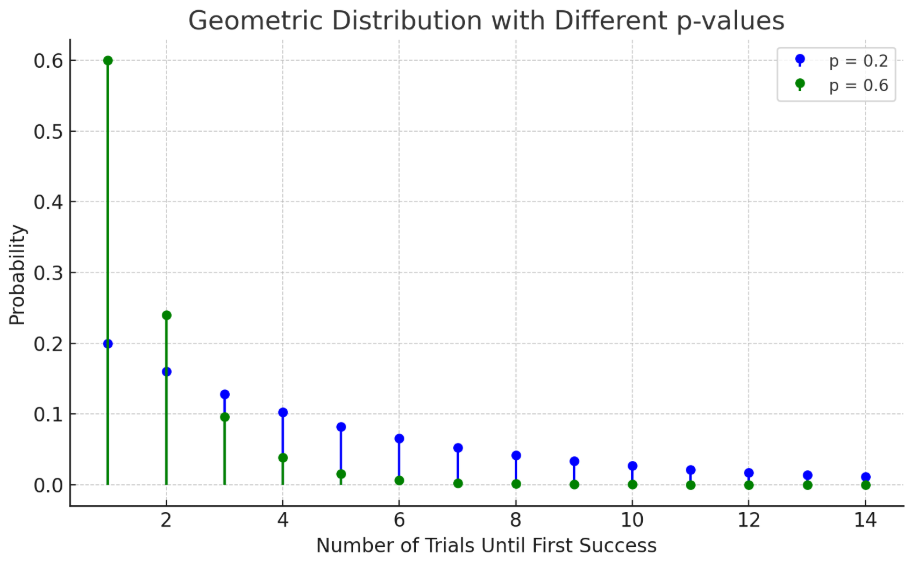
几何分布
进行多次相互独立的实验,每次成功的概率是 ,则达到一次成功所需要的实验次数的分布 可以表示为(实验 次需要 次失败和 1 次成功):
记作
低,分布更平,更可能导致更多的实验次数; 高,分布更陡,更可能在前几次就成功;
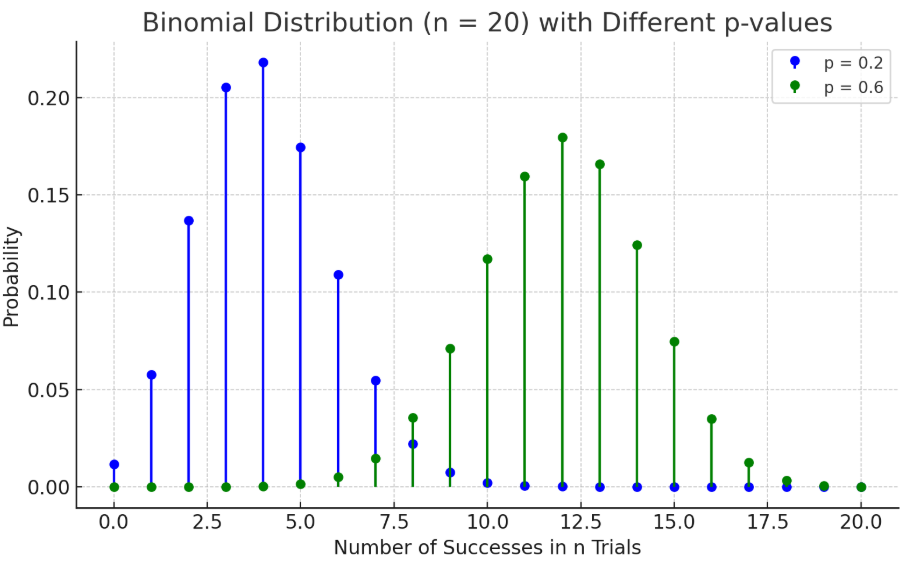
二项分布
记 为 次伯努利实验中成功的次数, 为试验成功的概率,则成功次数 服从以下分布:
记作 或者
越小,分布的峰值越偏左,集中在小值。 时分布对称。
伯努利分布
伯努利分布是二项分布的特例:
表示伯努利试验有没有发生我们关心的事件。概率质量函数:
常见于二分类问题中:
- 你已经观测到了数据
- 即某次试验给出了具体结果 或 。
- 此时 被当作 常数,不再是随机变量。
- 你把成功概率 视为未知参数,需要估计或推断
- 在频率学派里要做最大似然估计 (MLE)。
- 在贝叶斯框架里要与先验结合得到后验。
只要满足这两点,原本的 PMF 就自动变成了似然:
而对这个似然取对数就变成了交叉熵:
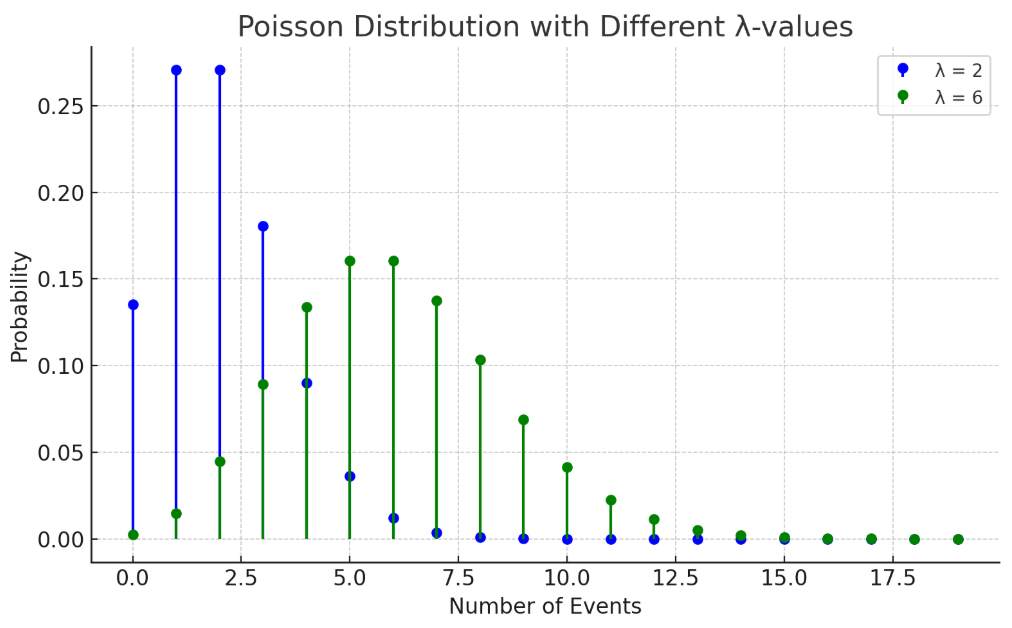
泊松分布
已知某个区间内,事件平均发生的次数 (非负实数,不一定得是整数),用 表示给定区间内事件发生的次数,则 服从泊松分布
-
:表示事件同时发生 次的强度;
-
:发生 次事件有很多顺序组合,而这些事件又是等价的,所以除以 来消重。
-
:是个归一化因子,用来确保所有可能值的概率总和是 1。它可以理解为“没有任何事件发生”的基本概率,也叫“零事件概率”。把 提到外面:
而这正是指数函数的泰勒级数展开式:
所以,
这说明整个概率分布是归一化的 —— 所有可能事件的概率加起来正好是 1。
记作 :
越小,事件发生的次数更集中在较小值,分布偏左,反之偏右。
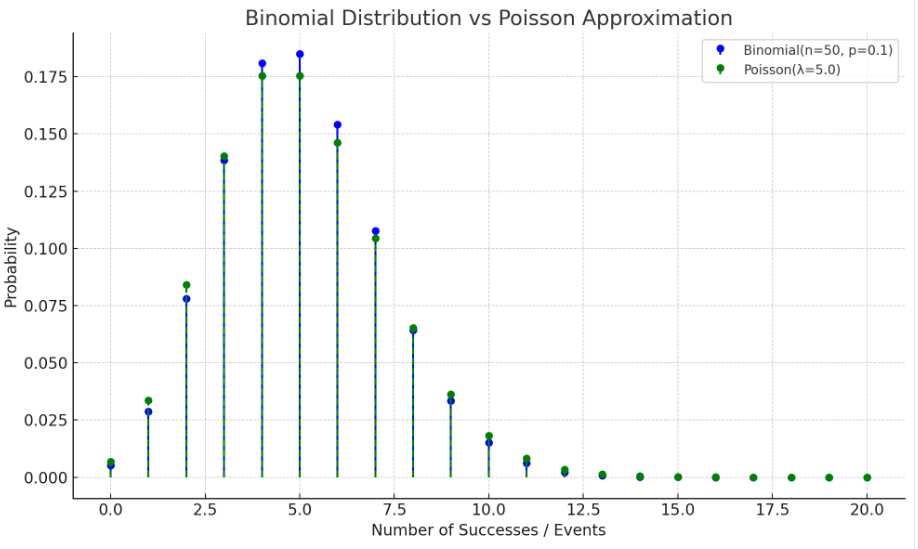
用泊松分布近似二项分布
当 很大且 很小时, 可以用于近似替代
比如 且 ,此时近似的泊松分布 。
Note
泊松分布可以由二项分布推导出来
设二项分布:
如果我们令:
- (无限多次试验,二项分布中式固定的试验次数,而在泊松分布中,连续的区间可以进行无限多次的试验)
- (每次成功概率很小,事件在无限细的时空中以极小概率独立发生。)
- 但保持 恒定(这是保持整个系统期望不变)
就可以推导出:
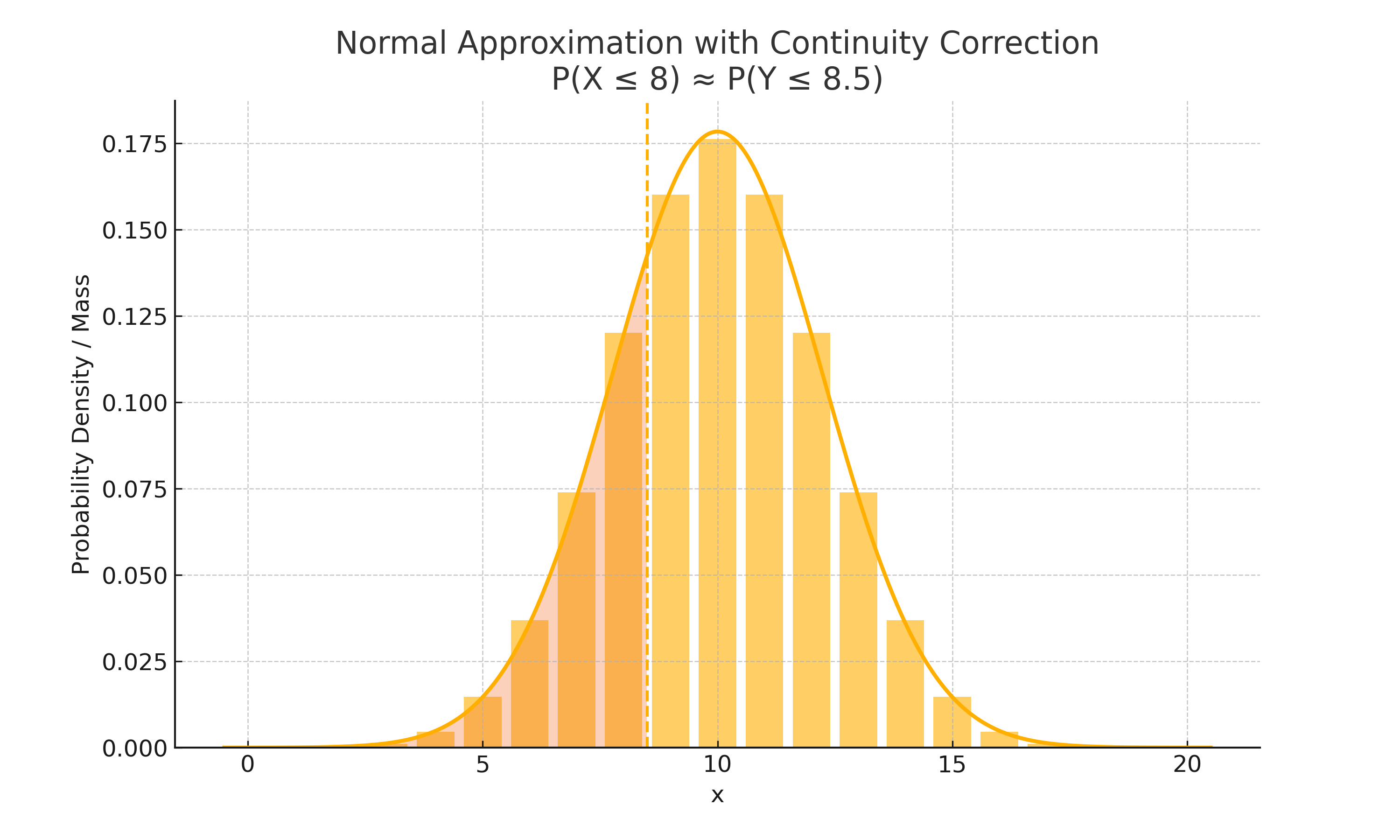
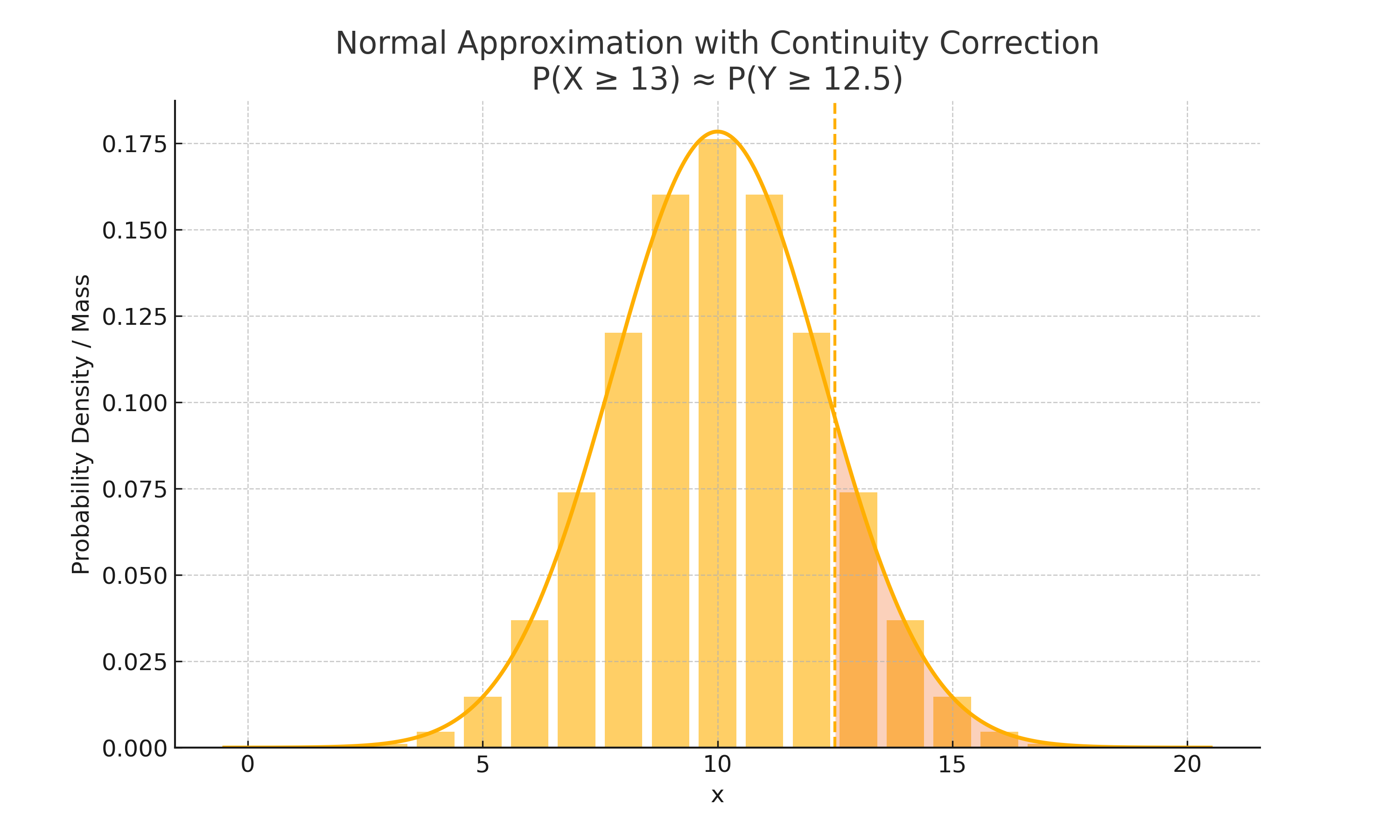
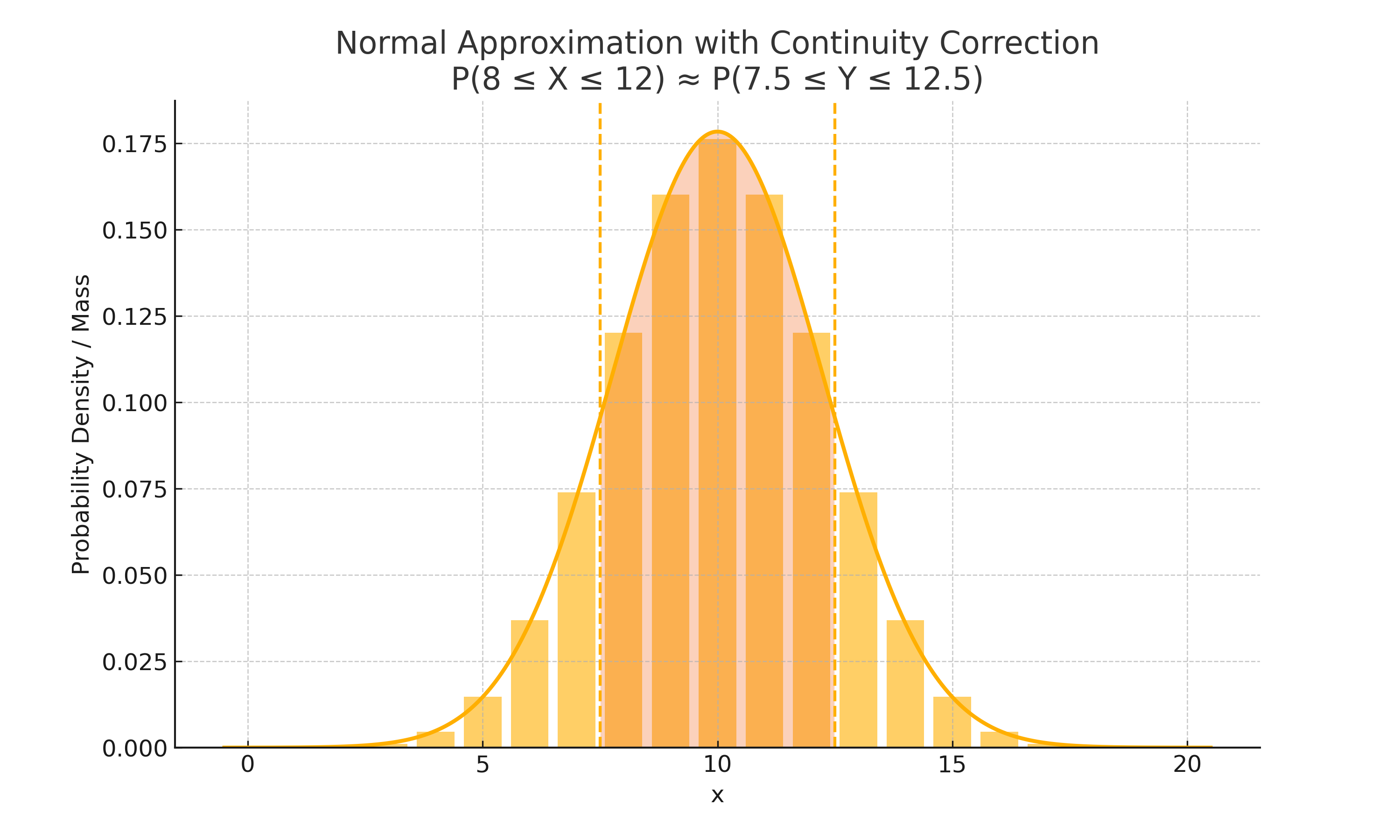
正态分布近似二项分布和泊松分布
当二项分布近似于对称时,可以用 来近似二项分布 。常见的条件是成功次数和失败的次数都要足够多,才能保持分布是大致对称的:
当泊松分布的参数 足够大时(通常 ),此时泊松分布趋近对称,可以用 近似 。
在用正态分布近似离散分布时,要进行连续修正: