Redis 数据结构

发表于 分类于 ， 本文字数： 3.3k

底层数据结构

SDS

SDS (Simple Dynamic String，简单动态字符串)，会缓存字符串的长度（无需像C语言的strlen那样计算char *的长度），可以自动扩展内存，以二进制的方式写入和读取，故可以存储任何字节数据：

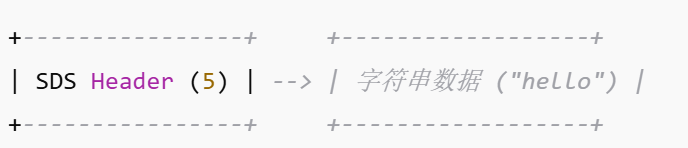
  1. EMBSTR 编码：是一种特殊的 SDS 优化，专门用于存储短字符串（<= 44 字节），**SDS 元数据和字符串内容分配在同一个连续内存块中。**任何修改会触发重新分配，所以本质上其是只读的（在重新分配时可能转为 RAW）。可以自动转化为正常的SDS(RAW)

    image-20250513202529576

  2. Raw 编码：普通 SDS，独立分配的 SDS 和字符串内容（> 44 字节）。SDS 元数据和字符串内容分配在两个内存块中。

    image-20250513202519619

Ziplist 和 Listpack

Ziplist

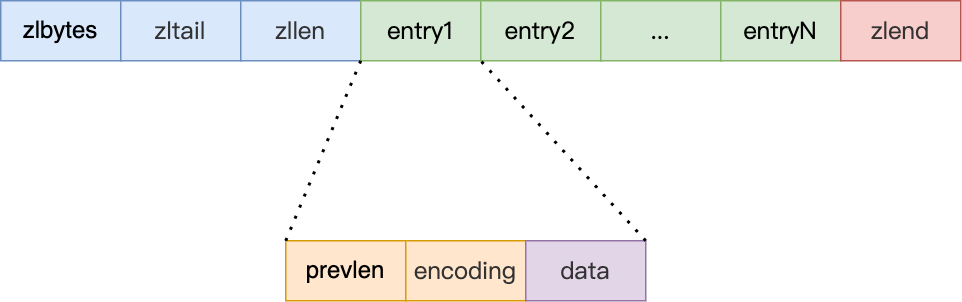
Ziplist 是一个紧凑的字节序列，按照以下结构存储：

  • zlbytes（4 字节）： 压缩列表的总字节数，用于快速扩展或释放内存。

  • zltail（4 字节）： 最后一个元素的偏移量，加速从尾部查找元素。

  • zllen（2 字节）： 列表中的元素数量。当超过 65535（2^16 - 1）时，表示无限制。

  • entries...： 列表中的各个元素，每个元素包含：

    • 前置长度（prevlen）： 前一个元素的长度（字节数，可以作为前向指针用于反向遍历）。
    • 编码长度（encoding）： 当前元素的编码类型和长度。
    • 实际数据（content）： 字符串或整数数据。
    1
    2
    3
    +---------+--------------+---------+
    | Prevlen | Encoding     | Content |
    +---------+--------------+---------+

  • zlend（1 字节）： 特殊标记，表示列表结束，固定为 0xFF。

为什么 Ziplist 不适合大数据？

  • 当 Ziplist 变得很长或元素频繁变化时：
    • 插入或删除需要移动大量数据，性能下降。
    • 容易导致 内存碎片。
    • 在插入和删除时需要修改前向指针。
img

listpack

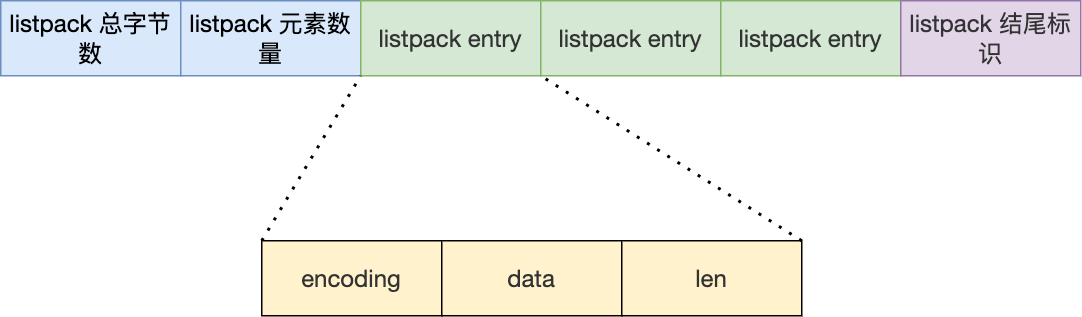
listpack 是直接使用字符数组 unsigned char * 实现的，不采用结构体。所以指向 listpack 类型的指针是 unsigned char * 类型的

img

  • lp_bytes（4 字节）： Listpack 的总字节数，用于快速扩展或释放内存。

  • lp_count（2 字节）： Listpack 中元素的数量（注意数量无法推导出总字节数）。

  • entries： Listpack 中的每个元素。Listpack 中的每个元素都包含：

    • 编码（encoding）
    • 数据（data）
    • 数据长度（length）

  • lp_end（1 字节）： 固定为 0xFF，表示列表结束。

listpack 相比 Ziplist

Ziplist 设计的失败之处在于元素存储的是prevlen并放在实际内容的前面，而不是存储curlen并放在当前内容的后面，这意味着在插入或删除元素时需要 重新计算并更新前向指针。

Quicklist

Quicklist 是一个 双向链表，其中每个节点都是一个 Listpack（紧凑列表）：

1
2
3
4
5
6
7
8
typedef struct quicklist {
quicklistNode *head;      // 链表头
quicklistNode *tail;      // 链表尾
unsigned long count;      // 列表中所有元素总数
unsigned int len;         // Quicklist 节点的数量（Listpack 数量）
int fill;                 // 每个 Listpack 的填充因子
unsigned int compress;    // Listpack 压缩级别
} quicklist;

img

1
2
3
4
5
6
7
8
9
10
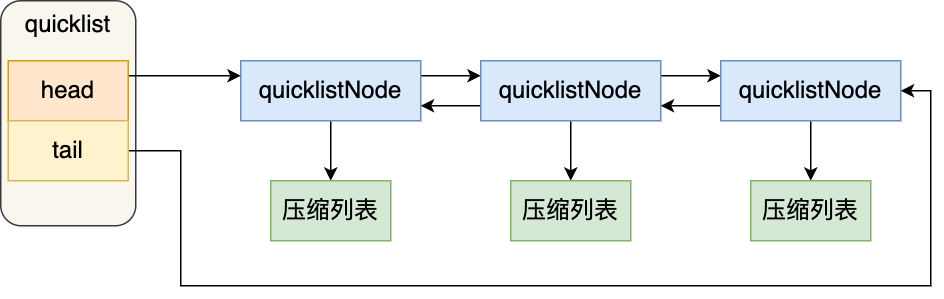
11
typedef struct quicklistNode {
 struct quicklistNode *prev;  // 前驱节点（双向链表）
 struct quicklistNode *next;  // 后继节点（双向链表）
 unsigned char *entry;        // 指向 Listpack 数据的指针
 unsigned int sz;             // Listpack 数据大小（字节）
 unsigned int count;          // Listpack 中的元素数量
 unsigned char encoding;      // 编码类型（Listpack）
 unsigned char container;     // 存储容器类型（Listpack）
 unsigned char recompress;    // 是否延迟压缩标记
 unsigned char attempted_compress; // 是否尝试压缩
} quicklistNode;

Quicklist 可以通过 fill 参数控制每个 Listpack 中的最大元素数量。

  • 如果 fill 值较小，每个 Listpack 存储的元素较少（高效插入删除）。
  • 如果 fill 值较大，每个 Listpack 存储的元素较多（节省内存）。

dict

基本属性

哈希表

  • Redis 使用 MurmurHash 或 DJB Hash 作为哈希函数将键转换为哈希值（hash）。
  • 通过哈希掩码将哈希值转换为索引（index = hash & (size - 1);）。哈希掩码（Hash Mask） 是 Redis HashTable 中通过 位运算 快速将哈希值转换为表索引的核心技术。哈希掩码 = 哈希表大小 - 1，并且哈希表大小始终是 2 的幂次方。
  • 如果两个键的哈希值相同，它们将被存储在相同的桶中（链表中）。新元素总是插入链表的头部。

HashTable 动态扩容

当哈希表中的键值对数量超过哈希表大小（负载因子 > 1），Redis 会自动扩容。扩容为原大小的 2 倍。

采用 渐进式 Rehash（rehash），避免一次性扩容带来的性能抖动。分批次（每次操作迁移一部分）地将键值对从旧表迁移到新表。

Redis 的 dict 类型实际上通过 dictht ht[2] 数组定义了两个哈希表，这样如果需要扩容，则在每次执行与 HashTable 相关的操作（如插入、删除、查询）时：

  • Redis 会将旧表（ht[0]）中的一个桶（bucket）迁移到新表（ht[1]）。
  • 在高并发情况下，每次操作只迁移一个桶，逐步完成。
  • 当所有桶都迁移到新表，旧表（ht[0]）会被释放，ht[1] 替代 ht[0] 成为新的主表

Intset

IntSet 是一个 紧凑的连续内存数组，专门用于存储整数。

1
2
3
4
5
6
typedef struct intset {
uint32_t encoding; // 当前整数编码类型（int16_t, int32_t, int64_t）
uint32_t length;   // 当前整数个数
int8_t contents[]; // 实际存储整数的数组（按升序排序，避免重复）
} intset;

整数集合升级：如果新元素的类型(int32 t)比整数集合现有所有元素的类型(int16_t)都要长时，整数集合需要先进行升级，也就是按新元素的类型(int32 t)扩展 contents 数组的空间大小，然后才能将新元素加入到整数集合里。步骤：空间扩容→从后往前转换原有元素→末尾放入新元素。

Skiplist

基本结构

img

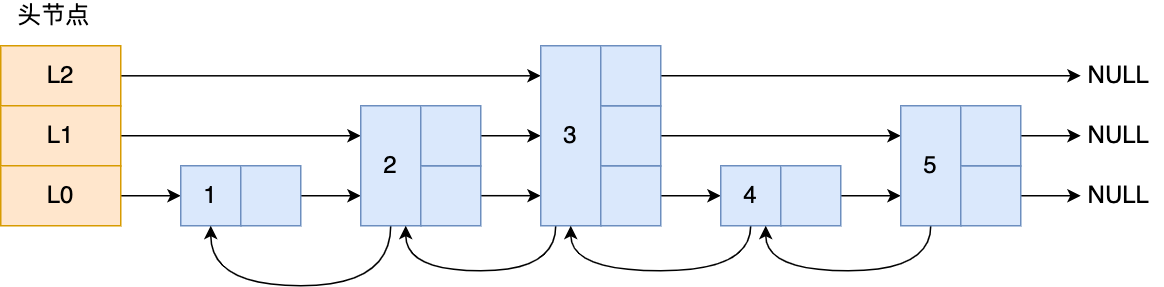
每个结点内有多个后向指针：头结点内拥有指向全部层第一个元素的头指针L0 ~ Ln，其他节点内根据其所在的层数拥有不同的指针数量。如果一个节点同时存在于 l 个层中，其就有 l 个后向的指针。

redis/src/t_zset.c at unstable · redis/redis

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 跳表的结构
typedef struct zskiplist {
// 头结点，注意只有一个，结点内有多个指针
struct zskiplistNode *header, *tail;
unsigned long length;
int level;
} zskiplist;

// 跳表每个结点的结构
typedef struct zskiplistNode {
//Zset 对象的元素值
sds ele;
//元素权重值，用于排序
double score;
//后向指针
struct zskiplistNode *backward;

// 一个数组，存储在每一层上其后向的指针及其跨度（指向后面的第几个元素）
struct zskiplistLevel {
  struct zskiplistNode *forward;
  unsigned long span;
} level[];
} zskiplistNode;

维持相邻层结点数量的关系

跳表的相邻两层的节点数量最理想的比例是 2:1，查找复杂度可以降低到 O(logN)。

通过几何分布来控制每个节点的层数：创建节点时候，会生成范围为[0-1]的一个随机数，如果这个随机数小于 0.25，那么层数就增加 1 层，然后继续生成下一个随机数，直到随机数的结果大于 0.25 结束。

1
2
3
4
5
6
7
8
9
10
11
12
/* Returns a random level for the new skiplist node we are going to create.
 * The return value of this function is between 1 and ZSKIPLIST_MAXLEVEL
 * (both inclusive), with a powerlaw-alike distribution where higher
 * levels are less likely to be returned. */
int zslRandomLevel(void) {
    static const int threshold = ZSKIPLIST_P*RAND_MAX;
    int level = 1;
    // 一直随机，直到有一个数超过了阈值
    while (random() < threshold)
        level += 1;
    return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}

这样的做法，相当于每增加一层的概率不超过 25%，层数越高，概率越低，层高最大限制是 64。

插入结点

  1. 从最高层开始逐层向下寻找合适的插入位置。

  2. 使用一个指针数组 update[] 保存每一层的插入位置的前一个元素，即 update[i]->level[i].forward = x。

  3. 更新反向指针

  4. 更新跳表元数据

Note

几何分布

它描述了 在一系列独立重复试验中，第一次成功前失败的次数。它是一种“第一次成功前的等待次数”分布。

每次成功的概率是 pp，那么失败次数 kk 的分布式 (1−p)kp(1-p)^kp 。也就是有 (1−p)kp(1-p)^kp 的概率失败 kk 次。

其期望为 (1−p)/p(1-p)/p

在跳表中，失败次数 + 1 即为当前节点的指针数，若其指针增加的概率是 0.25 (失败的概率，1−p1-p) ，其平均指针数是 (1−(1−p))/(1−p)+1=1/(1−p)(1-(1-p))/(1-p) + 1 = 1 / (1-p)

类型存储

String

String 的存储方法有三种：

  1. SDS (Simple Dynamic String，简单动态字符串)。

  2. INT编码：如果存储的字符串可以被解析为整数（如 “12345”），则 Redis 会自动将其存储为整数类型，以节省内存。

List

RPUSH 尾部插入，LPUSH 头部插入

Redis 3.2 之前：小于 512 个使用 Ziplist，大于 512 个使用双向链表

Redis 3.2 之后：全部使用 QuickList （快速列表），是一个 双端链表（Doubly Linked List） 与 Ziplist（压缩列表） 结合的优化结构。

Ziplist 是一种双向压缩列表，每个元素不仅记录自己的数据，还记录前一个元素的长度，从而实现双向遍历。

Hash

Redis 7.0 之前：较少（<512个键值对、每个键值对小于 64 byte）使用 Ziplist，否则使用 Hashtable (dict)

Redis 7.0 之后，把 Ziplist 换成了 listpack

Set

Redis 的 Set 类型有两种底层数据结构：

  1. IntSet（整数集合）： 当 Set 中的所有元素都是整数，且 Set 较小时。

  2. HashTable（哈希表）： 当 Set 中包含非整数元素或 Set 较大时。

ZSet

Redis 的 ZSet 类型在底层有 两种实现：

  1. Ziplist（压缩列表）或 listpack (redis 7.0+)： 适用于小型 ZSet（元素少，且分数和成员较短）。
  2. Skiplist（跳表）+ HashTable（哈希表）： 适用于大型 ZSet（元素多，或成员较长）。

**为什么 Redis 中有序集合（ZSet）使用跳表而不是红黑树？**因为跳表更简单，且在理论和实践上具有接近红黑树的性能。

  • 平衡树每个节点包含 2 个指针（分别指向左右子树），而跳表每个节点包含的指针数目平均为 1/(1−p)1/(1-p) （几何分布 - 维基百科，自由的百科全书），具体取决于参数 p 的大小。如果像 Redis里的实现一样，取 p=1/4，那么平均每个节点包含 1.33 个指针，比平衡树更有优势。
  • 在做范围查找的时候，跳表比平衡树操作要简单。在平衡树上，我们找到指定范围的小值之后，还需要以中序遍历的顺序继续寻找其它不超过大值的节点。如果不对平衡树进行一定的改造，这里的中序遍历并不容易实现。而在跳表上进行范围查找就非常简单，只需要在找到小值之后，对第 1 层链表进行若干步的遍历就可以实现。
  • 从算法实现难度上来比较，跳表比平衡树要简单得多。平衡树的插入和删除操作可能引发子树的调整，逻辑复杂，而跳表的插入和删除只需要修改相邻节点的指针，操作简单又快速。

Note

红黑树

性质

红黑树是一种 “近似平衡” 的二叉搜索树，满足以下 5 条性质：

  1. 每个节点要么是红色，要么是黑色。
  2. 根节点必须是黑色。
  3. 所有叶子节点（必定是 NIL，空节点）都是黑色。
  4. 红色节点的子节点必须是黑色（红色节点不能连续出现）。
  5. 从任一节点到其每个叶子节点的所有路径都必须具有相同数量的黑色节点（“黑色平衡”）。

插入

新节点总是红色

Case 1：新节点的父节点是黑色：无需调整，红黑树性质仍然保持。

Case 2：新节点的父节点是红色：必然会破坏“不能连续红色节点”这一性质。

  1. 父节点和叔节点都是红色（父节点和父节点的兄弟节点）：此时表示插入不影响平衡，但影响颜色，需要颜色翻转：父节点和叔节点都变成黑色，祖父节点变成红色，以祖父节点开始继续向上翻转颜色。
  2. 父节点是红色，叔节点是黑色：此时表示插入影响了平衡，不影响颜色，于是直接进行二叉树的旋转操作，包含 LL（左边长且插在左边的左边）、RR、LR（左旋父节点转为LL，右旋祖父节点）、RL。（插入位置和旋转方式是对应的，LL 既表示插在左边的左边，也表示需要左旋）

Case 3：根节点修复插入操作可能会导致根节点变红，要确保根节点始终为黑色：

近似平衡

  • 平衡标准比较宽松：没有一条路径会大于其他路径的2倍
  • 最大高度是 2 ∗ log2(n + 1)（100W个节点，红黑树最大树高40）
  • 搜索、添加、删除都是 O(logn) 复杂度，其中添加、删除都仅需 O(1) 次旋转调整