决策树：ID3、C4.5、CART 及其剪枝策略

发表于 2025-05-31 分类于机器学习本文字数： 2.5k

决策树的一般构建方法

创建一个根节点
从现有的所有叶子节点中，选择其中一个样本类别不全部相同且属性列表不为空的节点
从选择的节点的属性列表中根据一定算法选择一个属性
根据选择的属性的取值划分该节点中的样本，分裂出新的叶子节点，并将叶子节点的属性列表设置为当前属性列表去掉划分的属性

终止条件：

终止条件	描述
纯度达到	当前节点样本属于同一类别
属性用尽	没有剩余可用属性，如果仍不纯则使用节点内多数的标签
样本过少	当前样本量小于设定阈值
信息增益小	划分后信息增益不足
深度限制	达到最大深度限制

ID3 算法

使用信息增益作为划分属性的选择标准：信息增益=整个数据集的标签分布的熵-某个属性划分子集后的期望熵

对于包含 $C$ 个类别的数据集 $D$ ，设第 $i$ 个类别的分布为 $p_{i}$ ， $D$ 的熵定义为：

entropy (D) = - \sum_{i = 1}^{C} p_{i} \log p_{i}

按照属性 $A$ 划分数据集后，子集 $D_{1} \sim D_{m}$ 的熵的期望为：

entropy (D, A) = \sum_{i = 1}^{m} \frac{| D_{i} |}{| D |} entropy (D_{i})

以属性 $A$ 划分数据集 $D$ 带来的信息熵增益 $g a i n (D, A)$ 为：

Gain (D, A) = entropy (D) - entropy (D, A)

如果 $A$ 被选择为划分的属性，则会出现 $m$ 个分支。

ID4.5 的特点：

每次只选择一个属性做划分；
倾向于选择取值多的属性，因为那样会把数据集分成多而纯的子集，每个子集的熵都很低；
单变量决策树，每次只考虑一个属性，不考虑属性之间的相互关系

C4.5

信息增益率取代信息增益

使用 信息增益比例（Gain Ratio）来进行划分选择：

GainRatio (D, A) = \frac{Gain (D, A)}{IV (A)}

其中，IV（分裂信息）定义为（假设 $A$ 的取值范围为 $A$ ，而 $D_{a}$ 是按照取值 $a$ 划分的数据集)：

IV (A) = - \sum_{a \in A} \frac{| D_{a} |}{| D |} \log \frac{| D_{a} |}{| D |}

这样可以惩罚取值太多的属性，更公平地衡量不同属性的划分效果。其含义是按照 $A$ 划分数据集后，每个子集的 $A$ 的分布的熵的期望，IV 的计算与标签无关。

支持连续属性

对于连续属性 $A$ ，先将数据按 $A$ 的值排序，再在相邻样本之间找划分点 $θ$ ，通常选择其中点 $θ = \frac{a_{i} + a_{i + 1}}{2}$ 。

枚举所有可能划分点，对于每个候选点 $θ$ ，将样本划分为两组，最终选择使 GainRatio 最大的 $θ^{*}$ 与其他属性的 GainRatio 比较，如果其最大，则按照 $θ^{*}$ 划分该属性产生两个新节点。

处理缺失值

除了使用常用值、平均值之外，还可以按照概率分配：

为属性的每一个取值分配一个概率
在划分时，如果样本的划分属性缺失，则按照分配的概率选择分配到哪个节点

CART

Classification And Regression Tree

二叉树构建过程

分类任务，对于每个特征 $A$ ：

如果是离散特征：尝试将取值根据划分点 split 划分为两个集合。分别计算两组样本的标签的基尼指数，设一个节点中第 $i$ 个类别的分布是 $p_{i}$ ，共有 $K$ 个类别，则其样本集分布 $p$ 的基尼指数为：
$Gini (p) = 1 - \sum_{i}^{K} (p_{i}^{2})$
特别的，对于二分类的样本，如果第一个类的在样本集中的分布是 $p_{0}$ ，则：
$Gini (p) = 2 p_{0} (1 - p_{0})$
基尼指数越小，表示样本类别分布越均匀，表示样本集 $p$ 的不确定性更低。选择 split 时，选择能够最小化切分后的加权 Gini 的 split（ $N$ 表示节点总样本数， $N_{L} N_{R}$ 分别表示二分后两组样本的数量）：
${Gini}_{split} = \frac{N_{L}}{N} \cdot Gini (L) + \frac{N_{R}}{N} \cdot Gini (R)$
对所有属性都选择 split 并计算其划分后的加权基尼指数之后，选择最小的一个属性进行二叉分支。
如果是连续特征：枚举所有可能的划分值（见 C4.5连续属性)，同样计算他们的加权Gini，选择最小的划分点。

回归任务：与分类任务一样，但是把 Gini 换成 MSE，对于每个节点，其预测为其所有样本的均值，故其 MSE 为：

MSE = \frac{1}{n} \sum_{i = 1}^{n} (y_{i} - \bar{y})^{2}

递归地对所有的节点执行以上操作，直到达到终止条件。

终止条件

当前节点样本全属于同一类；
样本数量小于阈值；
树深达到 max_depth；
基尼指数下降太小（低于某个增益阈值）

剪枝策略

代价复杂度剪枝

CART 使用 代价复杂度剪枝（Cost Complexity Pruning）

构造完整树；
自底向上考虑是否“剪掉”某个子树，从叶子节点开始逐步考虑是否合并它们的父节点，从而剪掉“枝叶”部分，达到简化树结构的目的。
在决定是否剪掉以 $t$ 为根节点的子树 $T_{t}$ 的时候，我们考虑剪前后的损失函数 $C_{α} (T_{t})$ 和 $C_{α} (t^{'})$ ，其中 $t^{'}$ 表示 $t$ 合并了其子孙的所有样本，故叶子数量为 1， $α$ 是超参数，用于平衡损失和复杂度， $N_{t}$ 是以 $t$ 为根的子树的叶子中的样本数量：
$\begin{aligned} C_{α} (T_{t}) = & \sum_{t \in L e a v e s} N_{t} \cdot Error (t) + α \cdot | L e a v e s | \\ C_{α} (t^{'}) = & \sum_{t \in L e a v e s} N_{t} \cdot Error (t) + α \cdot 1 \end{aligned}$

在选择 $α$ 时，可以通过交叉验证选择最优的 $α$ 。

悲观剪枝

决策树后剪枝算法（三）悲观错误剪枝PEP-CSDN博客

通过比较“保留子树”与“剪成多数类叶节点”两种方案的估计错误率，如果剪枝后效果更好或复杂度更低，就执行剪枝。

以 $t$ 为根的子树的错误样本 $e (t)$ 表示少数类的样本数量，总样本 $n (t)$ 表示叶子中的样本数量。以节点 $t$ 为根节点的树其预测错误数服从二项分布 $e (t) \sim Binomial (n (t), e_{r e a l})$ ，其中 $e_{r e a l}$ 表示真实误差率。在实际剪枝时我们不知道真实的 $e_{r e a l}$ ，只知道观测到的错误样本数 $e (t)$ ，所以我们用 $e (t)$ 来悲观地计算 $e_{r e a l}$ ，下面的 $0.5$ 就是悲观项，也可以视作我们后面要在正态分布下估计误差上界的一个连续修正：

单节点分类错误率： $(e (t) + 0.5) / n (t)$
子树节点分类错误率是所有叶子节点的平均结果： $[\sum_{l \in T_{t}} (e (l) + 0.5)] / \sum_{l \in T_{t}} n (l)$

Note

根据中心极限定理，二项分布 $Binomial (n, p)$ 可以近似为正态分布 $N (n p, n p (1 - p))$ ，并且可以选择进行连续修正。

连续修正（continuity correction）是指在将离散分布（如二项分布）近似为连续分布（如正态分布）时，为了提高近似精度，对计算的临界值做出±0.5的调整。

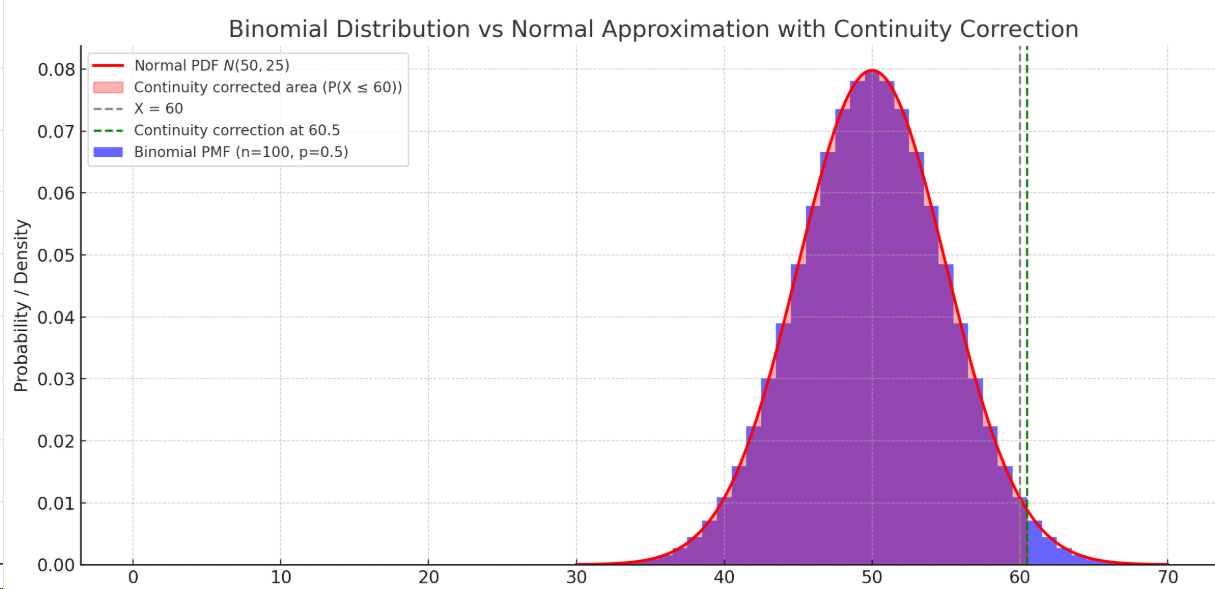
在上图中，我们试图用一个正态分布来近似一个二项分布。然而，在二项分布中， $P (X < 60)$ 的区域比正态分布中 $P (X < 60)$ 的区域多出一个角，为了补上这个角，我们需要给正态分布的区间 +0.5，即 $P (X < 60.5)$ 。参见图中的两条虚线，若不进行连续修正，红色曲线的面积会少覆盖一块区域；加上连续修正后，更贴近原本二项分布下的离散累积概率。

将二项分布近似为正态分布后，我们可以得到以 $t$ 为根的子树的错误数的标准差（ $\sqrt{n p (1 - p)}$ ）公式：

STD (e (T_{t})) = \sqrt{\frac{(\sum_{i = 1}^{L} e (i) + 0.5 L) (n (t) - \sum_{i = 1}^{L} e (i) - 0.5 L)}{n (t)}}

其中 $L$ 是叶子数量， $0.5$ 是连续修正项，表示在二项分布中采样的 $< e (i)$ 的概率接近其正态分布中 $< e (i) + 0.5$ 的概率密度的积分。判断是否剪掉以 $t$ 为根的子树的标准是：

\sum_{i = 1}^{L} e (i) + 0.5 L + z \cdot STD (e (T_{t})) \geq e (t) + 0.5

其中，左边是我们构造的原子树的误差数的上界， $z$ 控制置信水平，常见的比如 $z = 1.96$ 的时候置信水平为 95%，即我们以 95% 的置信水平构造了误差的上界。右侧是我们保守的剪枝后的误差数估计。以上不等式表明在这个保守估计下，剪枝是合理的。

剪枝过程：

先构建完整树；
自底向上遍历每个非叶子节点；
比较该子树的错误数上界与其下所有节点合并为叶节点后的估计错误数：
若满足上面的不等式就执行剪枝。

预剪枝

除了后剪枝外，也可以采用一些预剪枝策略，比如：

标准提升不足：若分裂节点后，判断是否分裂的标准的提升小于阈值（如基尼系数没有下降多少），则停止构建分支。
树的最大深度：限制树的层数。
节点样本数下限：若节点样本数小于设定阈值停止分裂，即便不纯。
类别纯度达标：若节点中某一类占比超过阈值则停止分裂，即便不纯。