统计学：假设检验

概论

假设检验是用于检验现有数据是否足以支持特定假设的方法。

• 原假设/零假设 $H_0$：想要拒绝的假设，是一种默认立场或初始假设。它通常是一个我们想要通过数据去“推翻”的假设；
• 备择假设 $H_1$：与原假设对立的假设，通常是我们希望通过数据来支持的假设。

在进行假设检验时，可能会出现两种错误：

• 弃真错误（第一类错误，$\alpha$ 错误）：原假设是正确的但是被拒绝了；
• 取伪错误（第二类错误，$\beta$ 错误）：原假设是假的但是被接受了，也就是备择假设是正确的但是没有被接受；

注意，我们不能靠举例子来证明一个命题是正确的，但是你可以靠举出一个反例来证明一个命题是错误的，所以在面对原假设时，我们只能预设其是错的，看看能不能找出其是错的证据（判断样本数据是否提供了足够证据来拒绝原假设）；不能证明出其是对的，我们只能说“我们不能拒绝原假设”。

拒绝域、临界值、显著性水平、p 值

显著性水平 $\alpha$ 衡量我们希望在样本结果的不可能程度达到多大时，拒绝原假设 $H_0$。用百分数表示。犯第一类错误的概率为 $\alpha$。

如果希望拒绝原假设时的证据更加充分，则应该设置更小的显著性水平，此时原假设被拒绝的概率更小，如果这么小的概率仍被拒绝，则说明拒绝它的时候证据更充分，也就是犯第一类错误的概率越小。反之，如果想要不拒绝原假设的时候证据更加充分，则应该设置更大的显著性水平。越想拒绝原假设

显著性水平 $\alpha$ 控制了拒绝域的大小，即当样本结果落在概率分布的哪个区域的时候，我们则认为该样本结果能够拒绝原假设。拒绝域的边界就是临界值。

对于单尾检验，拒绝域落在一侧，双尾检验则将拒绝域一分为二，并确保整个拒绝以相应概率反应这个检验水平，也就是两侧各占 $\alpha /2$。单尾检验通常是 $H_0$ 中带有 $\ge$ 或 $\le$，而双尾检验则是 $H_0$ 中带有 $\ne$ 。

p 值即某个小于等于拒绝域方向上的一个样本数值的概率，也就是用样本值在概率分布上确定一条线，然后这条线往拒绝域方向上的累积概率。利用样本进行计算，然后判定样本结果是否落在假设检验的拒绝域以内，也就是说，我们通过 p 值确定是否拒绝原假设。

$\beta$ 值、检验功效

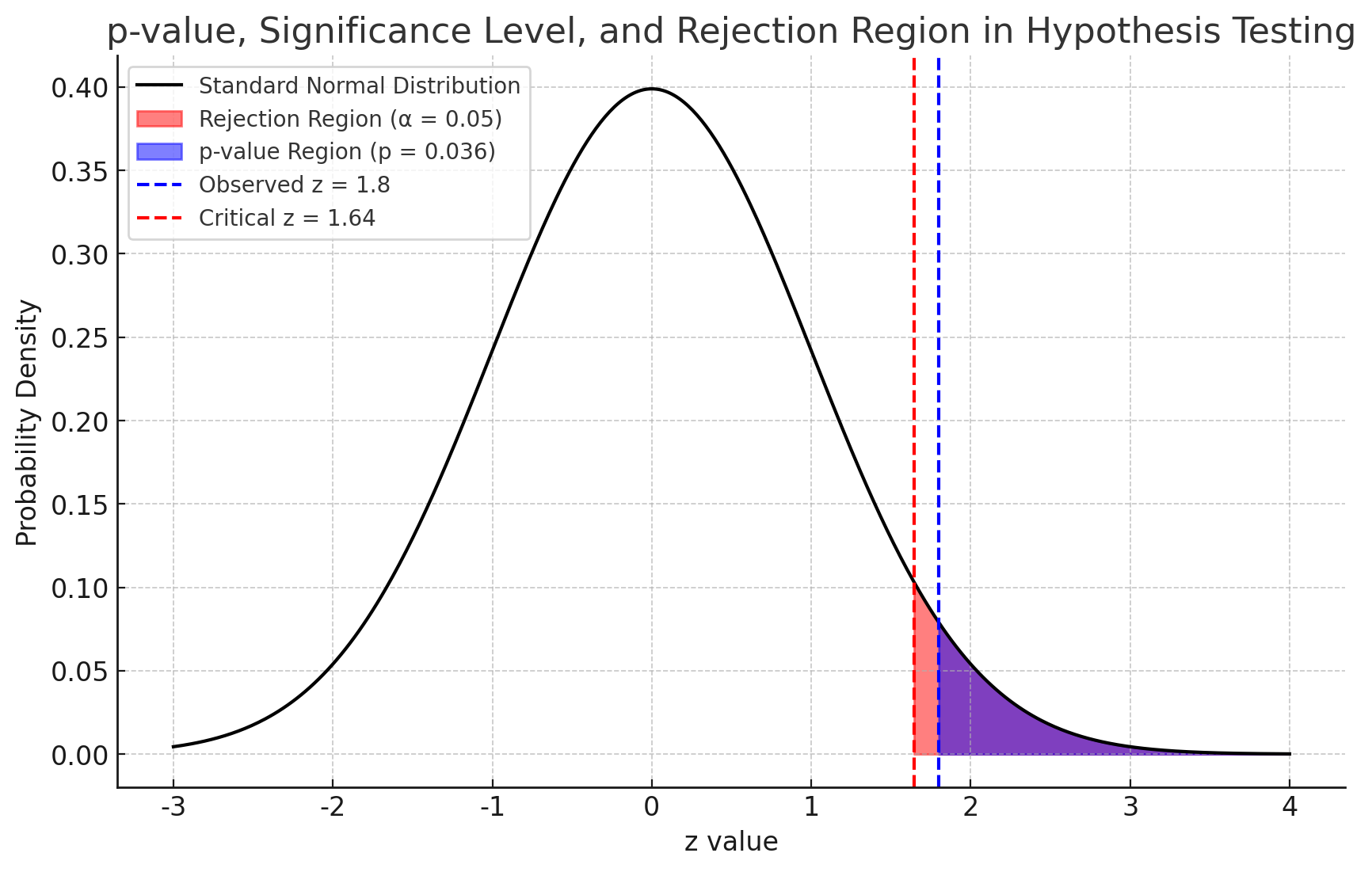
第一类错误的概率由 $\alpha$ 决定，类似的，我们将第二类错误的概率设为 $\beta$，即备择假设为真的情况下无法拒绝原假设的概率。首先需要求出样本中的接受原假设的数值范围（也就是拒绝域以外的范围），然后再计算 $H_1$ 取得这些数值的概率。

为接受 $H_1$ 指定一个确切的值，不然我们无法计算 $H_1$ 下的分布，比如如果我们 $H_1$ 假设了二项分布的成功概率是某个范围，我们无法把这个范围转为一个正态分布，只有确定了这个成功概率具体的值，我们才能将其转为正态分布。

我们可以计算 $H_0$ 无法拒绝的情况可能还包含着能够接收 $H_1$ 的情况，两者并不完全互斥。比如我们假设二项分布中的 P=0.8 和 P=0.9 分别作为 $H_0$ 和 $H_1$，那我们在无法拒绝 $H_0$ 的同时，我们也无法确定我们可以拒绝 $H_1$。

所以，我们在计算出 $H_0$ 的临界值对应的样本原来的值之后，我们看看这个值在 $H_1$ 所假设的分布中的 p 值，这表明在 $H_1$ 假设下我们有多大的概率也取得这个 p 值。

检验功效，指的是在 $H_0$ 为假的时候拒绝 $H_0$ 的概率，也就是我们正确拒绝了 $H_0$ 的概率，这和我们错误接受 $H_0$ 的概率互补，所以：

$$\text{检验功效}=1-\beta$$

z 检验

我们要检验样本均值是否服从一个假设的均值和方差。比如我们想检验整体的分布式是否是 $B(n,p)$，在 $n$ 比较大的时候，我们可以将其近似为 $N(np,npq)$，此时我们就有了假设所对应的均值和方差。

将我们样本的结果根据这个均值和方差进行标准化，表示该样本是总体正态分布标准化后的一个取样的值，称为 $z$ 统计量，即为：

$$z=\frac{X-\mu }{\sigma }$$

由于 $z$ 是标准正态分布的一个取样，我们就可以算出在标准正态分布中，$z$ 往拒绝域方向的所有事件的累积概率。

t 检验

t 分布

当你从正态总体中抽样，但不知道总体标准差，只能用样本标准差 $s$ 来估计时，统计量：

$$t=\frac{\overline{x}-\mu }{s/\sqrt{n}}$$

不再服从标准正态分布，而是服从一个 t 分布，其自由度为 $\nu =n-1$。

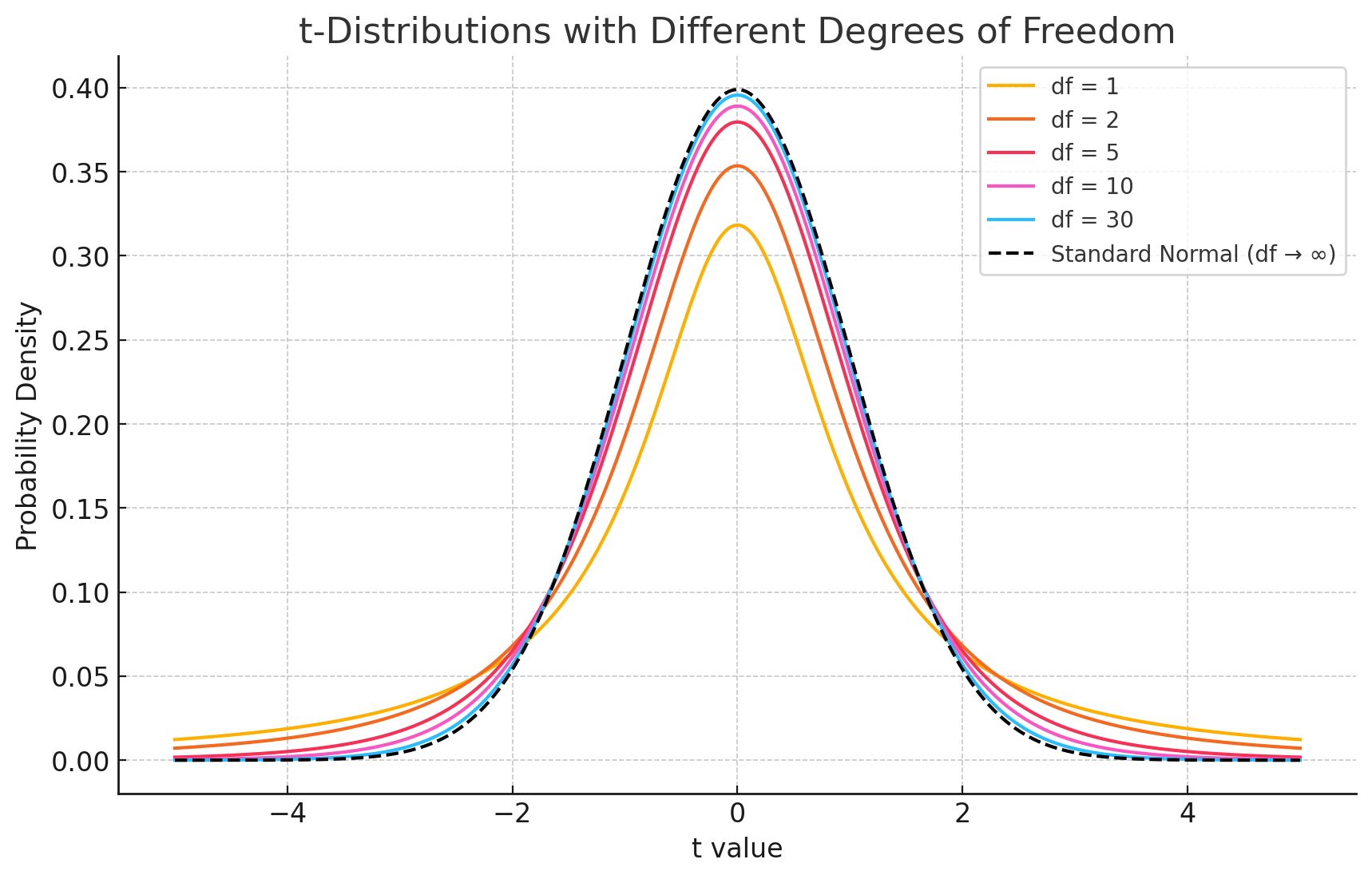
t 统计量

• 单样本均值检验（One-sample t-test）：用于检验 总体方差未知、正态数据或近似正态的 单样本的均值 是否与 已知的总体均值相等
• 两独立样本均值检验（Independent two-sample t-test）：用于检验 两对独立的 正态数据或近似正态的 样本的均值 是否相等，这里可根据总体方差是否相等分类讨论
• 配对样本均值检验（Dependent t-test for paired samples）：用于检验 一对配对样本的均值的差 是否等于某一个值

原假设 $H_0$：

• 单样本：$\mu ={\mu }_0$
• 独立样本：${\mu }_1={\mu }_2$
• 配对样本：差值均值 = 0

备择假设 $H_1$：

• 双尾：$\mu \ne {\mu }_0$
• 左尾：$\mu <{\mu }_0$
• 右尾：$\mu >{\mu }_0$

如果计算出的 $t$ 值落入拒绝域（或 p 值小于显著性水平 $\alpha$），就拒绝 $H_0$。

假设我们检验样本均值 $\overline{x}$ 与理论均值 ${\mu }_0$ 是否有显著差异：

$$t=\frac{\overline{X}-{\mu }_0}{s/\sqrt{n}}$$

其中：

• $\overline{X}$：样本均值
• ${\mu }_0$：原假设下的理论均值
• $s$：样本标准差
• $n$：样本大小
• 自由度：$\nu =n-1$

然后查 t 分布的临界值（$t_{\alpha ,\nu }$）或计算 p 值来做判断。

卡方检验（Chi-square Test）

$\chi^2 $ 分布

卡方分布可以校验观测结果和期望结果之间的差别是否存在显著性：

• 检验拟合优度，也就是一组给定数据与指定分布的吻合程度；
• 检验变量独立性，也就是检验变量之间是否存在关联；

卡方分布可以通过一个参数 $\nu$ 自由度来控制，自由度越高分布的峰值概率越低，峰值对应的 $X$ 越大，也就是这个分布更平。当 $\nu$ 为 1 或 2 的时候，分布的曲线是直接下降的，没有一个先上升后下降的过程。

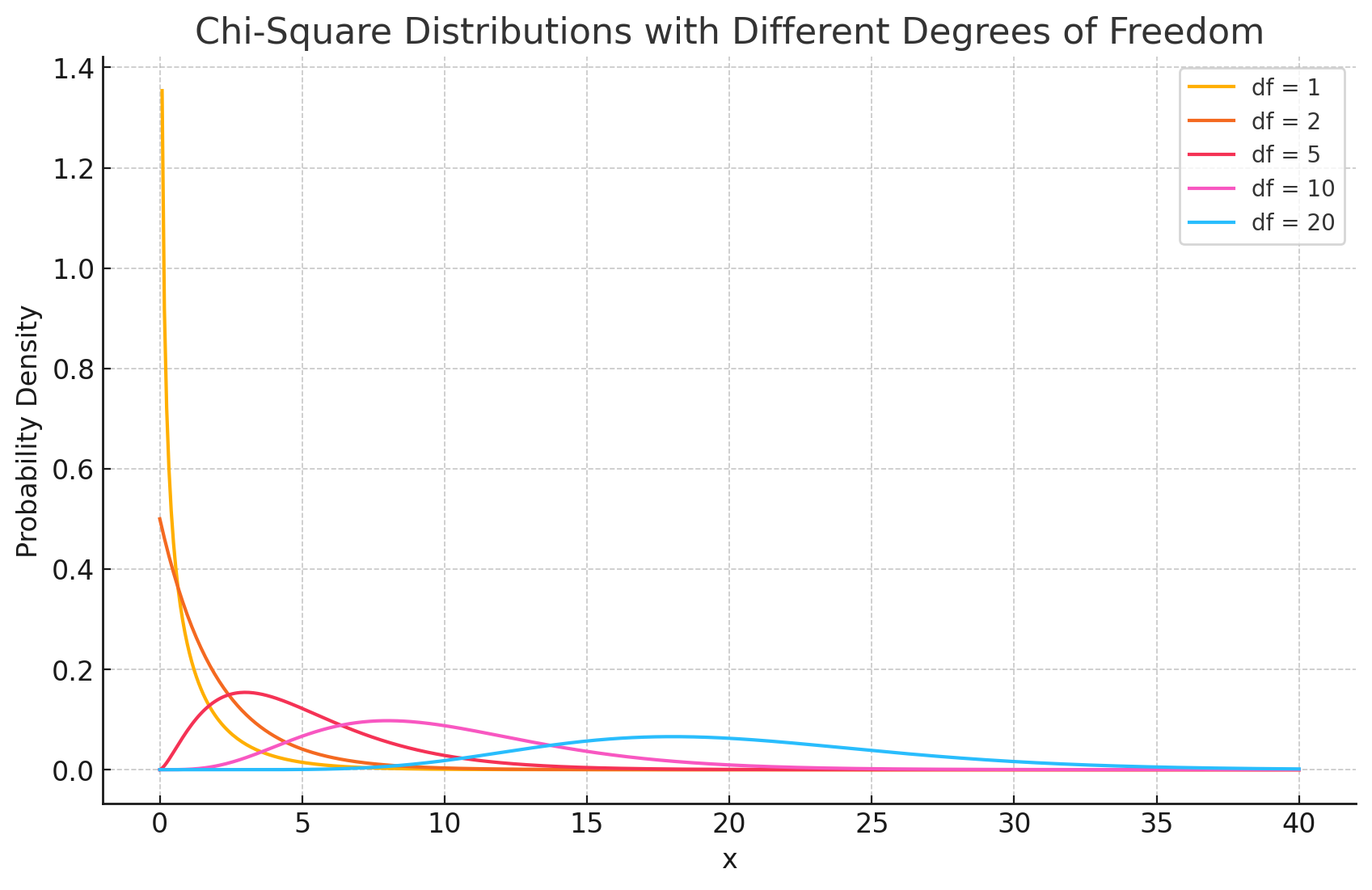
自由度 = 独立信息的数量 = 可自由变化的数据项数，比如总共有 $n$ 个项目，这 $n$ 个项目的总和是确定的，则我们只能任意指定 $n-1$ 个项目的值，剩下的那个值则用来满足总和。卡方分布是多个标准正态分布平方和构成的分布：

$${\chi }_{\nu }^2=Z_1^2+Z_2^2+\cdots +Z_{\nu }^2$$

其中每个 $Z_i\sim N(0,1)$ 是独立的标准正态变量。所以，自由度 $\nu$ 就是你累加了多少个独立的平方项。

拟合优度检验

检验观测频率是否符合期望分布。用 $O$ 表示观察到的频数，用 $E$ 表示期望的频率，则统计量的计算为，在 $H_0$ 假设为观察分布符合期望分布的时候，我们计算统计量为：

$${\chi }^2=\sum _i^k\frac{(O_i-E_i{)}^2}{E_i}$$

然后再根据这个统计量以及卡方分布的概率表来计算 p 值，并和显著性水平比较判断是否拒绝 $H_0$。

$k$ 个观测值的总和是固定的（因为样本总数 $n=\sum O_i$ 是已知的）自由度为：

$$\nu =k-1-r$$

其中 $r$ 为额外的约束数量，比如从数据中估计的参数个数，如估计了总体概率、均值等。

独立性检验

判断两个分类变量是否独立。假设：

$$H_0:\text{变量 A 与 B 相互独立}$$

和拟合优度检验不同的是，我们此刻已经没有了期望频数。为了得到期望频数，我们用联合观察频数在某个事件上的边缘总和作为该事件的期望频数，并进一步计算出概率。由于假设两个变量独立，所以我们可以用概率相乘作为两个事件同时发生的概率：

$$\begin{array}{rl}\text{期望频数}& =\text{总频数}\times P(A)\times P(B)\\ & =\text{总频数}\times \frac{A\text{ 发生的频数}}{\text{总频数}}\times \frac{B\text{ 发生的频数}}{\text{总频数}}\\ & =\frac{A\text{ 发生的频数}\times B\text{ 发生的频数}}{\mathrm{总}\mathrm{频}\mathrm{数}}\end{array}$$

有了期望频数后，对于所有联合事件，我们计算其期望分布，将结果和观测分布用于计算卡方值：

$${\chi }^2=\sum _{i=1}^h\sum _{j=1}^k\frac{(O_{ij}-E_{ij}{)}^2}{E_{ij}}$$

自由度为：

$$\nu =(h-1)\times (k-1)$$

A/B 测试

A 页面 vs B 页面，哪个带来更高的点击率？

原价格 vs 新价格，哪个转化率更高？

老广告 vs 新广告，哪个平均收入更高？

原假设 $H_0$：两组样本来自均值相同的总体（即 ${\mu }_A={\mu }_B$）

备择假设 $H_1$：两组总体均值不相等（${\mu }_A\ne {\mu }_B$）

计算 t 统计量（自由度为 $n+m-2$）：

$$t=\frac{{\overline{x}}_A-{\overline{x}}_B}{\text{SE}}$$

其中，$SE$ 标准误差衡量的是“在 $H_0$ 成立的前提下，两组样本均值的差的随机波动程度”。标准误差的公式（假设方差相等）：

$$SE=\sqrt{s_p^2(\frac{1}{n}+\frac{1}{m})}$$

其中：$n$、$m$：两组样本大小，$s_p^2$ 表示合并样本方差，即：

$$s_p^2=\frac{(n-1)s_A^2+(m-1)s_B^2}{n+m-2}$$

Note

每个样本方差 $s^2$ 本质上是：

$$s^2=\frac{1}{n-1}\sum _{i=1}^n(x_i-\overline{x}{)}^2$$

注意分母是 $n-1$，不是 $n$，这是因为我们用了 $\overline{x}$ 代替总体均值，消耗了一个自由度。现在，我们有两个组，分别估计出了 $s_A^2$ 和 $s_B^2$，它们估计的质量取决于样本量。样本量越大，方差估计越可靠，所以我们要做加权平均。于是：

$$s_p^2=\frac{(n-1)s_A^2+(m-1)s_B^2}{(n-1)+(m-1)}=\frac{(n-1)s_A^2+(m-1)s_B^2}{n+m-2}$$

参考资料

1. 深入浅出统计学（中文版）
2. 假设检验——这一篇文章就够了
3. Hypothesis Testing（假设检验） - 知乎
4. ChatGPT