生成式推荐：Meta HSTU 论文阅读笔记

推荐系统中的 Scaling Law

限制推荐系统走向 Scaling Law 的因素有：

1. 异构的特征：高基数的 id、cross、statistic 特征
2. 庞大的词表：亿级的动态词表，相比 10w 级的语言模型词表
3. 计算瓶颈：大语言模型的 token 量相比推荐系统来说算少的

异构数据统一成序列数据

对于 Sparse 特征：

1. 对于密集变化的特征，将其转化为主时间序列，例如用户交互过的物品序列等；
2. 对于很少变化的特征：同样转化为序列，但是在时间维度上进行去重

对于 Dense 特征，Dense 特征变化极快，导致其难以直接用序列来表示，然而，这些特征往往来源于 Sparse 特征，比如：物品近期的点击率，来源于用户与物品的交互行为。GRs 的做法是直接不使用 Dense 特征，而选择使用一个表达能力足够强的序列转换架构（sufficiently expressive sequential transduction architecture）。这通常指的就是像Transformer这样的模型。

Note

个人认为，这种处理和 DL 的发展路径是契合的。DL 的发展是伴随着特征工程的退化而进行的，早期的图像预处理往往多种多样，但是其带来的提升远不如模型结构升级所带来的提升。因为 DL 模型的更强大，允许我们提供更原始的数据给模型。模型在缺少一些归纳偏置的情况下，仍然能够学习到原始数据中的信息，甚至发现一些特征工程中无法挖掘的信息出来。

排序召回问题建模为序列转换问题

对于按时间排序的序列 $x_0,x_1,x_2,\dots ,x_{n-1}$，以及他们被观测到的时间 $t_0,t_1,t_2,\dots ,t_n$，序列转换任务将它们转换到相同特征空间下的序列 $y_0,y_1,y_2,\dots ,y_n$，$x_i\in \mathbb{X},y_i\in \mathbb{X}\cup \{\mathrm{\varnothing }\}$。当 $y_i=\mathrm{\varnothing }$ 的时候表明其 undefined。

用 ${\mathrm{\Phi }}_i$ 表示提供给用户的内容，用户可能通过行为 $a_i$ 来回应 ${\mathrm{\Phi }}_i$，${\mathrm{\Phi }}_i\in {\mathbb{X}}_c\in \mathbb{X}$，$a_i\in \mathbb{X}$，对于一个在不断成长的平台来讲，$\mathbb{X}$ 和 ${\mathbb{X}}_c$ 都不是稳定的。

对于排序任务，其本质上是想预测用户会对给定的内容做出什么样的行为，

排序

在常见的自回归预测模型中，往往在最后阶段，候选物品（候选词）才与历史信息发生交互。比如，Transformer 中，在最后经过 MLP 才映射出下一个 token 的 logits，再通过 softmax 取到。在 GRs 中，作者希望 ${\mathrm{\Phi }}_{i+1}$ 和历史特征（序列中已经存在了的特征）尽早地开始交互。所以，使用以下的形式来建模问题：

$$p(a_{i+1}\mid {\mathrm{\Phi }}_0,a_0,{\mathrm{\Phi }}_1,a_1,\dots ,{\mathrm{\Phi }}_i,a_i,{\mathrm{\Phi }}_{i+1})$$

可以看到，${\mathrm{\Phi }}_i$ 物品和 $a_i$ 动作交错放置在序列里面，而序列的下一步 ${\mathrm{\Phi }}_{i+1}{a}_{i+1}$ 中，直接把 ${\mathrm{\Phi }}_{i+1}$ 作为历史特征的一部分，也就是直接加入序列中，预测的目标则是 $a_{i+1}$，具体是使用一个小网络，将 ${\mathrm{\Phi }}_i$ 所在的输出转成 Multi-task 预测。

Note

很巧妙的建模方式。在转为自回归预测的时候，并没有直接用 $a_i$ 或直接用 ${\mathrm{\Phi }}_i$ 来做序列，因为无论选择这两者中的任何一种，都会使得模型在最后阶段才映射到候选物品的 ID 空间，无法尽早地让候选与历史行动进行交互。选择交错摆放的方式，将候选物品作为历史的一部分，这样在 Attention 等操作中，候选物品就会与上下文进行交互，有助于进行建模。

召回

和排序不同，召回的时候，（内容，行为）作为一个二元组，是序列的一个基本单元：

$$({\mathrm{\Phi }}_i,a_i)i=0,\dots ,n_c-1$$

召回的目标是，将上面的序列转为目标序列（注意上面是从 ${\mathrm{\Phi }}_0$ 开始的，下面是从 ${\mathrm{\Phi }}_1$ 开始的，类似于 Next-Token Prediction）：

$${\mathrm{\Phi }}_1^{\prime },\dots ,{\mathrm{\Phi }}_{n_c-1}^{\prime },\mathrm{\varnothing }i=1,\dots ,n_{c-1}$$

${\mathrm{\Phi }}_i^{\prime }$ 和 ${\mathrm{\Phi }}_i$ 的关系是：如果 ${\mathrm{\Phi }}_i$ 对应的行为 $a_i$ 是正向的，则 ${\mathrm{\Phi }}_i^{\prime }={\mathrm{\Phi }}_i$，否则 ${\mathrm{\Phi }}_i^{\prime }=\mathrm{\varnothing }$，表示未被定义。这与自回归预测不同，因为 ${\mathrm{\Phi }}_{i+1}$ 不一定是 ${\mathrm{\Phi }}_0,\cdots ,{\mathrm{\Phi }}_i$ 的监督信号，也就是其预测目标不一定是 ${\mathrm{\Phi }}_{i+1}$，而也有可能是 $\mathrm{\varnothing }$。

网络结构

前置知识

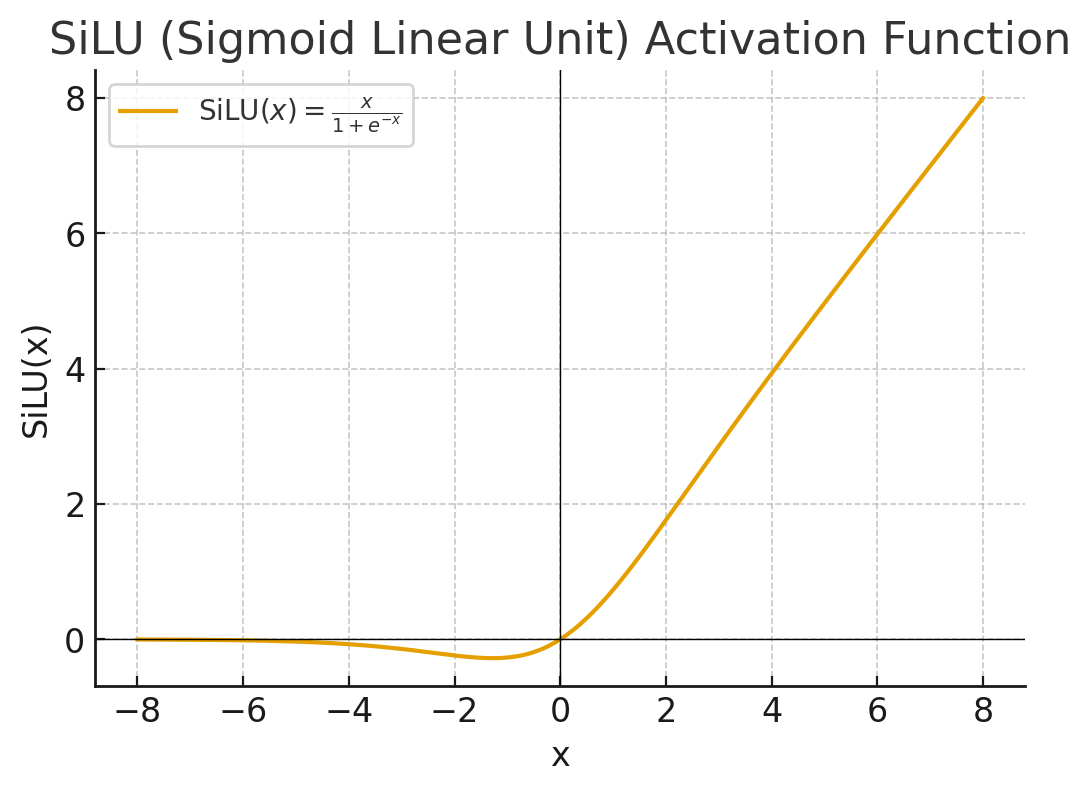
SiLU

2017 年提出的激活函，用 x 乘以 Sigmoid(x)

$$\text{SiLU}(x)=\frac{x}{1+e^{-x}}=x\cdot \sigma (x),\sigma (x)=\frac{1}{1+e^{-x}}$$

Relative Attention Bias

Attention Bias 就是指在注意力打分矩阵里 人为地加上一个偏置项 $B$：

$$\text{Attention}(Q,K,V)=\text{softmax}(\frac{Q{K}^{\mathrm{\top }}}{\sqrt{d}}+B)V$$

Relataive Attention Bias 指的是 位置偏置 (Relative Position Bias)，在 Transformer-XL, T5, GPT-NeoX 等里常见：

在计算注意力时加上相对位置相关的偏置，每个相对位置的差值都会有一个独立的可学习的参数 $b_{i-j}$ 控制，组成偏置矩阵 $B$：

$${\alpha }_{ij}=\frac{Q_i{K}_j^{\mathrm{\top }}}{\sqrt{d}}+b_{i-j}$$

其中 $b_{i-j}$ 依赖于相对位置差。

Swin Transformer之相对位置编码详解

Forward

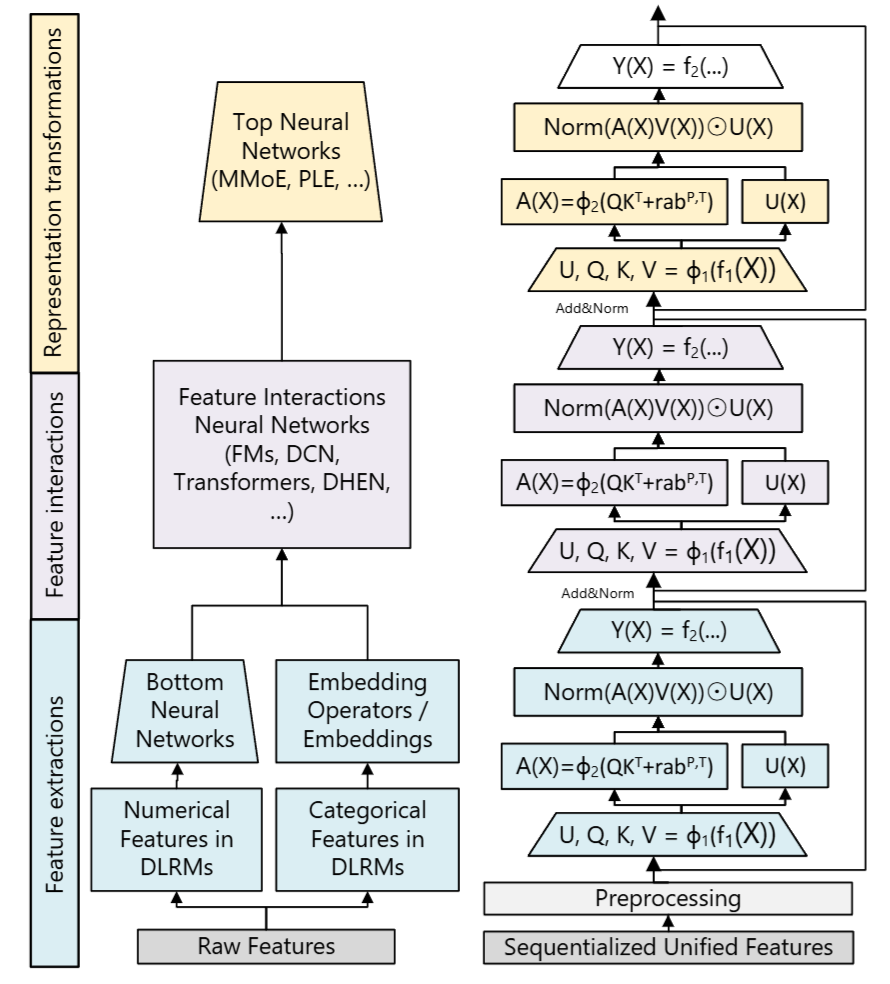
对于每个 HSTU 块，其内就是一个门控注意力模块：

1. 对于输入 $X$，使用一个激活函数为 ${\varphi }_1$ 的 MLP 将其映射后，切分成四个变量：$U,Q,K,V$（和 Transformer 不同，Transformer 中 QKV 是 3 个不同的网络投影出来的）：

   $$U(X),Q(X),K(X),V(X)=\text{Split}({\varphi }_1(f_1(x)))$$
   • $U$ gating weights
   • $Q,K,V$: Attention 的 $QKV$
   • $f_1$ 表示一个线性层，即 $f_1(X)=X{W}_1+b_1$

2. Pointwise Aggregated Attention: 点式聚合注意力：

   $$A(X)V(X)={\varphi }_2(Q(X)K(X{)}^T+{\text{rab}}^{p,t})V(X)$$

   这步与 Transformer 的 Self Attention 相似，但是有以下不同点：

   1. 不使用 Softmax；

   2. 加入了 ${\text{rab}}^{p,t}$ 相对位置注意力偏置；

   Note

   为什么不使用 Softmax 计算 Attention

   1. Softmax Attention 会强制所有注意力权重在 $[0,1]$ 且和为 1。在生成式推荐场景中，序列很长，如果用 Softmax，权重被挤压到少数几个 token，长序列信息很容易被稀释甚至遗忘。激活函数则允许权重保持独立尺度，不必满足概率分布约束。
   2. 虽然softmax激活函数在结构上对噪声具有鲁棒性，但其在流式数据场景中对非稳定的词汇表的适应性较差
   3. 减少计算开销，Softmax Attention 的计算是 $O(n^2)$，还需要数值稳定化处理（减最大值再 exp）。激活函数 Attention 只需要线性变换 + 点积 + 激活，计算复杂度更低，对超长用户行为序列更友好。

3. Point-wise 转换：

   $$Y(X)=f_2(Norm(A(X)V(X))\odot U(X))$$

   由于不使用 Softmax，在 $A(X)V(X)$ 之后，来需要进行 Layer Norm 来稳定训练。

   在这之后，并没有像 Transformer 接一个 FFN，所以每个块里面只有门控注意力。

   这里其实是用 Gated Attention Unit (GAU) 代替了 FFN，参考 《Transformer Quality in Linear Time》论文解读 - 知乎

将每个块作残差块，用残差连接串联起来，块与块之间使用 Add 后 Norm，形成了 HSTU 的 Forward Pass。

训练阶段的行为序列

训练时，用随机长度策略对用户的行为序列进行压缩，而在推理时，仍然使用完整的用户序列。

符号定义

对用户 $j$，其历史交互内容可以表示为一个序列

$$(x_i{)}_{i=0}^{n_{c,j}},$$

其中 $n_{c,j}$ 表示用户 $j$ 与内容交互的总次数。在所有用户中，定义所有用户中最大历史长度为

$$N_c=\underset{j}{max}{n}_{c,j}.$$

从原始序列中可以构造一个长度为 $L$ 的子序列，记为

$$(x_{i_k}{)}_{k=0}^L,$$

其中 $\{i_k\}$ 为从原序列中选取的索引集合。

随机长度 Stochastic Length, SL

根据用户历史长度 $n_{c,j}$ 决定是否对输入序列进行截断，当用户历史较短时（小于阈值 $N_c^{\alpha /2},\alpha \in (1,2]$），直接使用完整序列作为模型输入：

$$(x_i{)}_{i=0}^{n_{c,j}},\text{if }{n}_{c,j}\le N_c^{\alpha /2}.$$

当用户历史较长（即 $n_{c,j}>N_c^{\alpha /2}$）时，引入随机化的序列选择策略，有 $1-\frac{N_c^{\alpha }}{n_{c,j}^2}$ 的概率使用一个长度为 $N_c^{\alpha /2}$ 的子序列：

$$(x_{i_k}{)}_{k=0}^{N_c^{\alpha /2}},$$

可以看到，当某个用户的行为序列越长时，其使用子序列的概率越高。该子序列从原始序列中随机采样得到。相应的，有 $\frac{N_c^{\alpha }}{n_{c,j}^2}$ 的概率仍然使用完整序列，避免用户没有见过完整的长序列。$\alpha$ 越大，被采样的概率越低。

复杂度：这样之后，用户行为序列的最长长度从 $N_c$ 变成接近 $N_c^{\alpha /2}$ (因为过长的行为序列几乎必然被裁剪)，则 Attention 的计算复杂度从 $O(N_c^2)d$ 减少到了 $O(N_c^{\alpha }d)$

$\alpha$ 参数的影响

定义一下 Sparsity，

$$\text{Sparsity}=1-\frac{\text{Average Sequence Length}}{\text{Max Sequence Length}}$$

也就是 Tensor 里面是 padding 的元素的比例。可以看到，$\alpha$ 参数越低，倾向于让序列变得更短，稀疏度越高。在使用稀疏优化的算子的时候，训练速度会更快，然而也会导致模型无法学习到长程依赖。

子序列采样

有效的子序列采样可以提高模型的表现，用 $f_i$ 表示 Recency：

$$f_i=t_n-t_i$$

• $t_n$: 当前时刻（或最后一次交互时刻）。
• $t_i$: 第 $i$ 个物品交互的时刻。
• $f_i$ 越小，代表行为发生得越近（越新鲜）。

论文对比了三种从长序列中提取 $L$ 个物品的方法，这其实是在权衡 短期兴趣（Short-term） 与 长期兴趣（Long-term） 。

1. Greedy Selection（贪心选择）：直接选 $f_i$ 最小的 $L$ 个物品，也就是直接截断旧的行为序列，是传统序列推荐的标准做法，但它彻底丢弃了用户的长期兴趣。

2. Random Selection（随机选择）：从历史 $S$ 中均匀随机抽取 $L$ 个。虽然覆盖了全生命周期，但引入了太多噪声。推荐系统通常具有很强的时间相关性，昨天的行为比去年的行为重要得多。随机采样打破了这种先验知识。

3. Feature-Weighted Selection（特征加权选择 ）：根据 $f_i$ 构造一个概率分布来采样

   $$P(\text{select }i)\propto 1-\frac{f_{n,i}}{\sum f}$$

   核心思想是概率与时间差成反比，这是一个软衰减策略。行为越近（$f_i$ 小），被选中的概率越高。行为越远（$f_i$ 大），被选中的概率越低，但不会为零。重点保留了近期偏好，模型主要关注当下的意图，但也保留了长尾信号：模型有机会回忆起很久以前的行为。

   除此之外，这种加权采样其实是一种隐式的数据增强。同一个用户在不同的 Epoch 中，被采样出的子序列是略有不同的（最近的总是都在，但远期的行为会随机出现），这极大地防止了模型过拟合。